Question

已知函数f（x）=ax²+1，g（x）=x³+bx，其中a＞0，b＞0．
（Ⅰ）若曲线y=f（x）与曲线y=g（x）在它们的交点P（2，c）处有相同的切线（P为切点），求a，b的值；
（Ⅱ）令h（x）=f（x）+g（x），若函数h（x）的单调递减区间为[]，求：
（1）函数h（x）在区间（一∞，-1]上的最大值M（a）；
（2）若|h（x）|≤3，在x∈[-2，0]上恒成立，求a的取值范围．

Answer 1

解：（I）f（x）=ax²+1（a＞0），则f'（x）=2ax，k₁=4a，g（x）=x³+bx，则f'（x）=3x²+b，k₂=12+b，
由（2，c）为公共切点，可得：4a=12+b  ①
又f（2）=4a+1，g（2）=8+2b，
∴4a+1=8+2b，与①联立可得：a=，b=5．
（Ⅱ）（1）由h（x）=f（x）+g（x）=x³+ax²+bx+1，
则h′（x）=3x²+2ax+b，
因函数h（x）的单调递减区间为[]，∴当x∈[]时，3x²+2ax+b≤0恒成立，
此时，x=-是方程3x²+2ax+b=0的一个根，得3（-）²+2a（-）+b=0，得a²=4b，
∴h（x）=x³+ax²+a²x+1
令h'（x）=0，解得：x₁=-，x₂=-；
∵a＞0，∴-＜-，列表如下：

x	（-∞，-）	-	（-，-）	-	（-，+∞
h′（x）	+	?	-	?	+
h（x）	?	极大值	?	极小值	?

∴原函数在（-∞，-）单调递增，在（-，-）单调递减，在（-，+∞）上单调递增
①若-1≤-，即a≤2时，最大值为h（-1）=a-；
②若-＜-1＜-，即2＜a＜6时，最大值为h（-）=1
③若-1≥-时，即a≥6时，最大值为h（-）=1．
综上所述：当a∈（0，2]时，最大值为h（-1）=a-；当a∈（2，+∞）时，最大值为h（-）=1．
（2）由（1）知，函数h（x）在（-∞，-）单调递增，在（-，-）单调递减，在（-，+∞）上单调递增
故h（-）为极大值，h（-）=1；h（-）为极小值，h（-）=-；
∵|h（x）|≤3，在x∈[-2，0]上恒成立，又h（0）=1．
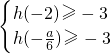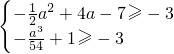∴即，解得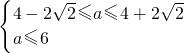
∴a的取值范围：4-2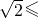a≤6．

分析：（I）根据曲线y=f（x）与曲线y=g（x）在它们的交点（2，c）处具有公共切线，可知切点处的函数值相等，切点处的斜率相等，故可求a、b的值；
（II）（1）根据函数h（x）的单调递减区间为[]得出a²=4b，构建函数h（x）=f（x）+g（x）=x³+ax²+a²x+1，求导函数，利用导数的正负，可确定函数的单调区间，进而分类讨论，确定函数在区间（-∞，-1）上的最大值．
（2）由（1）知，函数h（x）在（-∞，-）单调递增，在（-，-）单调递减，在（-，+∞）上单调递增
，从而得出其极大值、极小值，再根据|h（x）|≤3，在x∈[-2，0]上恒成立，建立关于a的不等关系，解得a的取值范围即可．
点评：本题考查导数知识的运用，考查导数的几何意义，考查函数的单调性与最值，解题的关键是正确求出导函数和应用分类讨论的方法．