
分析 (1)先求函数的导数,根据导数和函数的单调性的关系即可求出,
(2)要求若f(x)≥2tx-$\frac{1}{{x}^{2}}$在x∈(0,1]内恒成立,即转化为2t≤x+$\frac{1}{{x}^{3}}$-$\frac{2lnx}{x}$在x∈(0,1]内恒成立,只需求h(x)=x+$\frac{1}{{x}^{3}}$-$\frac{2lnx}{x}$x∈(0,1]内的最小值即可.
解答 解:(1)证明:函数的定义域为(0,+∞),f′(x)=2x-$\frac{2}{x}$=$\frac{2(x+1)(x-1)}{x}$,
由f′(x)>0,得x>1,由f′(x)<0,得0<x<1,
所以,函数f(x)在区间(1,+∞)上单调递增.
(2)由f(x)≥2tx-$\frac{1}{{x}^{2}}$对x∈(0,1]恒成立,得2t≤x+$\frac{1}{{x}^{3}}$-$\frac{2lnx}{x}$.
令h(x)=x+$\frac{1}{{x}^{3}}$-$\frac{2lnx}{x}$,则h′(x)=$\frac{{x}^{4}-2{x}^{2}-3+2{x}^{2}lnx}{{x}^{4}}$,
因为x∈(0,1],所以x4-3<0,-2x2<0,
2x2lnx<0,x4>0,
所以h′(x)<0,
所以h(x)在(0,1)上为减函数.
所以当x=1时,h(x)=h(x)=x+$\frac{1}{{x}^{3}}$-$\frac{2lnx}{x}$,有最小值2,得2t≤2,
所以t≤1,故t的取值范围是(-∞,1].
点评 本题考查了利用导数求闭区间上函数的最值,以求函数恒成立问题,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
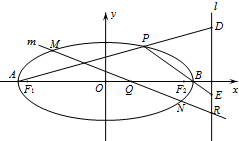 椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.
椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com