
【题目】在以下命题中,不正确的个数为( )
①![]() 是
是![]() ,b共线的充要条件;②若
,b共线的充要条件;②若![]() ∥
∥![]() ,则存在唯一的实数λ,使
,则存在唯一的实数λ,使![]() =λ
=λ![]() ;③对空间任意一点O和不共线的三点A,B,C,若
;③对空间任意一点O和不共线的三点A,B,C,若![]() =2
=2![]() -2
-2![]() -
-![]() ,则P,A,B,C四点共面;④若{
,则P,A,B,C四点共面;④若{![]() ,
,![]() ,
,![]() }为空间的一个基底,则{
}为空间的一个基底,则{![]() +
+![]() ,
,![]() +
+![]() ,
,![]() +
+![]() }构成空间的另一个基底;⑤ |(
}构成空间的另一个基底;⑤ |(![]() ·
·![]() )·
)·![]() |=|
|=|![]() |·|
|·|![]() |·|
|·|![]() |.
|.
A. 2
【答案】C
【解析】
利用不等式|![]() |﹣|
|﹣|![]() |≤|
|≤|![]() |等号成立的条件判断①即可;利用
|等号成立的条件判断①即可;利用![]() 与任意向量共线,来判断②是否正确;利用共面向量定理判断③是否正确;根据不共面的三个向量可构成空间一个基底,结合共面向量定理,用反证法证明即可判断④;代入向量数量积公式验证即可判断⑤.
与任意向量共线,来判断②是否正确;利用共面向量定理判断③是否正确;根据不共面的三个向量可构成空间一个基底,结合共面向量定理,用反证法证明即可判断④;代入向量数量积公式验证即可判断⑤.
对①,∵向量![]() 、
、![]() 同向时,
同向时,![]() ,∴不满足必要性,∴①错误;
,∴不满足必要性,∴①错误;
对②,当![]() 为零向量,
为零向量,![]() 不是零向量时,不存在λ使等式成立,∴②错误;
不是零向量时,不存在λ使等式成立,∴②错误;
对③,若P,A,B,C四点共面,则存在唯一![]() 使得
使得![]() .
.
则![]() ,即
,即![]() .
.
又![]() =2
=2![]() -2
-2![]() -
-![]() ,所以
,所以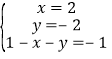 ,方程无解,故③错误;
,方程无解,故③错误;
对④,用反证法,若{![]() }不构成空间的一个基底;
}不构成空间的一个基底;
设![]() x
x![]() (x﹣1)
(x﹣1)![]()
![]() x
x![]() (1﹣x)
(1﹣x)![]() ,即
,即![]() ,
,![]() ,
,![]() 共面,∵{
共面,∵{![]() }为空间的一个基底,∴④正确;
}为空间的一个基底,∴④正确;
对⑤,∵|(![]() )
)![]() |=|
|=|![]() |×|
|×|![]() |×|cos
|×|cos![]() ,
,![]() |×|
|×|![]() |≤|
|≤|![]() ||
||![]() ||
||![]() |,∴⑤错误.
|,∴⑤错误.
故选:C.


科目:高中数学 来源: 题型:
【题目】数列{an}为递增的等差数列,数列{bn}满足bn=anan+1an+2(n∈N*),设Sn为数列{bn}的前n项和,若a2![]() ,则当Sn取得最小值时n的值为( )
,则当Sn取得最小值时n的值为( )
A.14B.13C.12D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 的动直线
的动直线![]() 于椭圆相交于
于椭圆相交于![]() 两点,当直线
两点,当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得弦长为
截得弦长为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在与点
上是否存在与点![]() 不同的定点
不同的定点![]() ,使得直线
,使得直线![]() 和
和![]() 的倾斜角互补?若存在,求
的倾斜角互补?若存在,求![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由实数构成的等比数列{an}满足a1=2,a1+ a3+ a5=42.
(I)求数列{an}的通项公式;
(II)求a2+ a4+ a6+…+ a2n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,现从参与调查的人群中随机选出20人的样本,并将这20人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示
,得到的频率分布直方图如图所示

(1)求a的值.
(2)根据频率分布直方图,估计参与调查人群的样本数据的![]() 分位数(保留两位小数).
分位数(保留两位小数).
(3)若从年龄在![]() 的人中随机抽取两位,求两人恰有一人的年龄在
的人中随机抽取两位,求两人恰有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)令![]() ,试讨论
,试讨论![]() 的单调性;
的单调性;
(2)若对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由![]() ,对函数求导,研究导函数的正负得到单调性即可;(2)由条件可知
,对函数求导,研究导函数的正负得到单调性即可;(2)由条件可知![]() 对
对![]() 恒成立,变量分离
恒成立,变量分离![]() ,令
,令![]() ,求这个函数的最值即可.
,求这个函数的最值即可.
解析:
(1)由![]() 得
得![]()
当![]() 时,
时, ![]() 恒成立,则
恒成立,则![]() 单调递减;
单调递减;
当![]() 时,
时,  ,令
,令 ,
,
令 .
.
综上:当![]() 时,
时, ![]() 单调递减,无增区间;
单调递减,无增区间;
当![]() 时,
时,  ,
, 
(2)由条件可知![]() 对
对![]() 恒成立,则
恒成立,则
当![]() 时,
时, ![]() 对
对![]() 恒成立
恒成立
当![]() 时,由
时,由![]() 得
得![]() .令
.令![]() 则
则
 ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]()
所以![]() ,从而可知
,从而可知![]() .
.
综上所述: 所求![]() .
.
点睛:导数问题经常会遇见恒成立的问题:
(1)根据参变分离,转化为不含参数的函数的最值问题;
(2)若 ![]() 就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为
就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为![]() ,若
,若![]() 恒成立
恒成立![]() ;
;
(3)若![]() 恒成立,可转化为
恒成立,可转化为![]() (需在同一处取得最值) .
(需在同一处取得最值) .
【题型】解答题
【结束】
22
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴的极坐标系中,直线
轴的非负半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·绍兴仿真考试)已知数列{an}的奇数项依次构成公差为d1的等差数列,偶数项依次构成公差为d2的等差数列(其中d1,d2为整数),且对任意n∈N*,都有an<an+1,若a1=1,a2=2,且数列{an}的前10项和S10=75,则d1=________,a8=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过椭圆![]() 的右焦点F作直线
的右焦点F作直线![]() 交椭圆于M、N两点,H为线段MN的中点,且OH的斜率为
交椭圆于M、N两点,H为线段MN的中点,且OH的斜率为![]() ,设点
,设点![]()
![]() 求该椭圆的方程;
求该椭圆的方程;
![]() 若点P是椭圆上的动点,求线段PA的中点G的轨迹方程;
若点P是椭圆上的动点,求线段PA的中点G的轨迹方程;
![]() 过原点的直线交椭圆于B、C两点,求
过原点的直线交椭圆于B、C两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com