
| A. | [-1,1] | B. | [-1,$\frac{1}{3}}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}}$] | D. | [-1,-$\frac{1}{3}}$] |
分析 求出f(x)的导数,由题意可得f′(x)≥0恒成立,设t=cosx(-1≤t≤1),即有5-4t2+3at≥0,对t讨论,分t=0,0<t≤1,-1≤t<0,分离参数,运用函数的单调性可得最值,解不等式即可得到所求范围.
解答 解:函数f(x)=x-$\frac{1}{3}$sin2x+asinx的导数为f′(x)=1-$\frac{2}{3}$cos2x+acosx,
由题意可得f′(x)≥0恒成立,
即为1-$\frac{2}{3}$cos2x+acosx≥0,
即有$\frac{5}{3}$-$\frac{4}{3}$cos2x+acosx≥0,
设t=cosx(-1≤t≤1),即有5-4t2+3at≥0,
当t=0时,不等式显然成立;
当0<t≤1时,3a≥4t-$\frac{5}{t}$,
由4t-$\frac{5}{t}$在(0,1]递增,可得t=1时,取得最大值-1,
可得3a≥-1,即a≥-$\frac{1}{3}$;
当-1≤t<0时,3a≤4t-$\frac{5}{t}$,
由4t-$\frac{5}{t}$在[-1,0)递增,可得t=-1时,取得最小值1,
可得3a≤1,即a≤$\frac{1}{3}$.
综上可得a的范围是[-$\frac{1}{3}$,$\frac{1}{3}$].
另解:设t=cosx(-1≤t≤1),即有5-4t2+3at≥0,
由题意可得5-4+3a≥0,且5-4-3a≥0,
解得a的范围是[-$\frac{1}{3}$,$\frac{1}{3}$].
故选:C.
点评 本题考查导数的运用:求单调性,考查不等式恒成立问题的解法,注意运用参数分离和换元法,考查函数的单调性的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
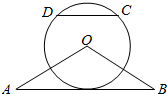 如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,$\frac{1}{2}$OA为半径作圆.
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,$\frac{1}{2}$OA为半径作圆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
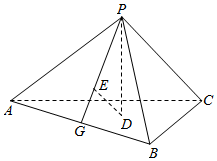 如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.
如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,1) | C. | (-1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com