练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数.

    （1）讨论函数在定义域内的极值点的个数；

    （2）若函数在处取得极值，对任意的恒成立，，求实数的取值范围.

    【答案】（1）详见解析；（2）.

    【解析】试题分析：（Ⅰ）求出原函数的导函数，然后对 分类讨论导函数的符号，在 时由导函数在不同区间内的符号得到原函数的单调性，从而求得函数的极值点；
    （Ⅱ）由函数 在 处取得极值求得，代入函数解析式，进一步代入 ，分离参数后构造函数，利用导数求其最小值后得答案．

    试题解析：

    （1）.

    当时，在上恒成立，函数在单调递减，所以在上没有极值点；

    当时，由得，由得

    所以在上递减，在递增，即在处有极小值.

    综上：当时，在上没有极值点；

    当时，在上有一个极值点.

    （2）因为函数在处取得极值，所以.

    因为，令，可得在上递减，在上递增.

    ∴ ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在测试中，客观题难度的计算公式为，其中为第题的难度， 为答对该题的人数， 为参加测试的总人数．现对某校高三年级120名学生进行一次测试，共5道客观题．测试前根据对学生的了解，预估了每道题的难度，如下表所示：

    题号

    1

    2

    3

    4

    5

    考前预估难度

    0.9

    0.8

    0.7

    0.6

    0.4

    测试后，从中随机抽取了10名学生，将他们编号后统计各题的作答情况，如下表所示（“√”表示答对，“×”表示答错）：

    学生编号 题号

    1

    2

    3

    4

    5

    1

    ×

    √

    √

    √

    √

    2

    √

    √

    √

    √

    ×

    3

    √

    √

    √

    √

    ×

    4

    √

    √

    √

    ×

    ×

    5

    √

    √

    √

    √

    √

    6

    √

    ×

    ×

    √

    ×

    7

    ×

    √

    √

    √

    ×

    8

    √

    ×

    ×

    ×

    ×

    9

    √

    √

    ×

    ×

    ×

    10

    √

    √

    √

    √

    ×

    （Ⅰ）根据题中数据，将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表，并估计这120名学生中第5题的实测答对人数；

    题号

    1

    2

    3

    4

    5

    实测答对人数

    实测难度

    （Ⅱ）从编号为1到5的5人中随机抽取2人，求恰好有1人答对第5题的概率；

    （Ⅲ）定义统计量，其中为第题的实测难度， 为第题的预估难度．规定：若，则称该次测试的难度预估合理，否则为不合理．判断本次测试的难度预估是否合理.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中， 分别是角的对边，且，若， ，则的面积为( )

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-5：不等式选讲

    已知函数.

    （1）若，求不等式的解集；

    （2）若方程有三个不同的解，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线过点，且方向向量为；在以为极点， 轴的正半轴为极轴的极坐标系中，圆的极坐标方程为.

    （1）求直线的参数方程；

    （2）若直线与圆相交于、两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

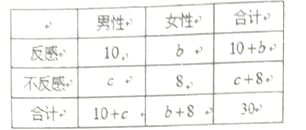
    【题目】“中国式过马路” 存在很大的交通安全隐患，某调查机构为了解路人对“中国式过马路”的态度是否与性别有关，从马路旁随机抽取30名路人进行了问卷调查，得到了如图的列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是.

    （1）求列联表中的的值；
    （2）根据列联表中的数据，判断是否有把握认为反感“中国式过马路”与性别有关？

    参考公式：，

    临界值表：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知， 是的导函数.

    （1）求的极值；

    （2）证明：对任意实数，都有恒成立；

    （3）若在时恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校高三数学备课组为了更好地制定复习计划，开展了试卷讲评后效果的调研，从上学期期末数学试题中选出一些学生易错题，重新进行测试，并认为做这些题不出任何错误的同学为“过关”，出了错误的同学为“不过关”，现随机抽查了年级50人，他们的测试成绩的频数分布如下表：

    期末分数段

    人数

    5

    10

    15

    10

    5

    5

    “过关”人数

    1

    2

    9

    7

    3

    4

    （1）由以上统计数据完成如下列联表，并判断是否有的把握认为期末数学成绩不低于90分与测试“过关”有关？说明你的理由：

    分数低于90分人数

    分数不低于90分人数

    合计

    “过关”人数

    “不过关”人数

    合计

    （2）在期末分数段的5人中，从中随机选3人，记抽取到过关测试“过关”的人数为，求的分布列及数学期望．

    下面的临界值表供参考：

    0.15

    0.10

    0.05

    0.025

    2.072

    2.706

    3.841

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线方程为.

    （1）求该双曲线的实轴长、虚轴长、离心率；

    （2）若抛物线的顶点是该双曲线的中心，而焦点是其左顶点，求抛物线的方程.

    查看答案和解析>>

    同步练习册答案