
分析 (Ⅰ)依题意:曲线C上的任意点到点F(1,0)的距离等于到直线x=-1的距离,由此能求出曲线C的方程.
(Ⅱ)设过点M(m,0),(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2),设l的方程为x=ty+m,与抛物线方程联立,得y2-4ty-4m=0,利用$\overrightarrow{FA}•\overrightarrow{FB}$<0恒成立,由此能求出m的取值范围.
解答 解:(Ⅰ)依题意:曲线C上的任意点到点F(1,0)的距离等于到直线x=-1的距离,
∴曲线C的方程是y2=4x,x>0.
(Ⅱ)设过点M(m,0),(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2),
设l的方程为x=ty+m,
与抛物线方程联立,得y2-4ty-4m=0,
△=16t2+16m>0,y1+y2=4t,y1y2=-4m,①
又$\overrightarrow{FA}$=(x1-1,y1),$\overrightarrow{FB}$=(x2-1,y2),
∵$\overrightarrow{FA}•\overrightarrow{FB}$<0,∴(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+y1y2<0,②
等价于$\frac{1}{16}$(y1y2)+2y1y2-$\frac{1}{4}$[(y1+y2)2-2y1y2]+1<0
由①式,m2-6m+1-4t2<0,
∵4t2≥0
∴只需m2-6m+1<0即可.
即:3-2$\sqrt{2}$<m<3+2$\sqrt{2}$,
∴所求m的取值范围为3-2$\sqrt{2}$<m<3+2$\sqrt{2}$.
点评 本题考查曲线方程的求法,考查满足条件的实数是否存在的判断,解题时要认真审题,注意等价转化思想和函数方程思想的合理运用.


科目:高中数学 来源: 题型:填空题
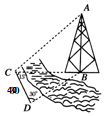 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.测得∠BCD=15°,∠BDC=30°,CD=40米,并在点C测得塔顶A的仰角为60°,则塔高AB=20$\sqrt{6}$米.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.测得∠BCD=15°,∠BDC=30°,CD=40米,并在点C测得塔顶A的仰角为60°,则塔高AB=20$\sqrt{6}$米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | [1,+∞) | C. | (0,2] | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
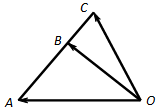
| A. | $\overrightarrow{c}$=3$\overrightarrow{a}$-$\overrightarrow{b}$ | B. | $\overrightarrow{c}$=3$\overrightarrow{b}$-$\overrightarrow{a}$ | C. | $\overrightarrow{c}$=$\frac{3}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$ | D. | $\overrightarrow{c}$=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com