
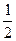 ×
×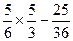 ,S正=22=4,
,S正=22=4,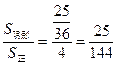 .
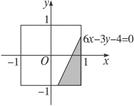
.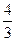 ,即6a-3b>4的数组数N1,
,即6a-3b>4的数组数N1,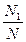 .可以发现,试验次数越多,概率P越接近
.可以发现,试验次数越多,概率P越接近 .
.

科目:高中数学 来源:不详 题型:解答题
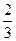 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为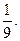
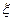 ,求
,求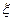 的分布列与均值E
的分布列与均值E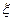 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
, ,
, 的频率分布直方图中对应的小矩形的高分别是
的频率分布直方图中对应的小矩形的高分别是 ,问所取的40名学生的成绩不低于
,问所取的40名学生的成绩不低于 分的共有多少人?
分的共有多少人? 分的学生中任取2人为一组(不分先后),求至少有1人的成绩在
分的学生中任取2人为一组(不分先后),求至少有1人的成绩在 内的概率.
内的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
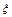 为成活沙柳的株数,数学期望E(
为成活沙柳的株数,数学期望E(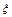 )为3,标准差
)为3,标准差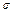 为
为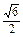 .
.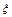 的概率分布;
的概率分布;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
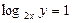 的概率为( ).
的概率为( ). A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com