练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．计算：C${\;}_{4}^{3}$+C${\;}_{5}^{3}$+…+C${\;}_{10}^{3}$=329．

    分析 利用组合数公式${C}_{n}^{m+1}$+${C}_{n}^{m}$=${C}_{n+1}^{m+1}$进行化简即可．

    解答 解：C${\;}_{4}^{3}$+C${\;}_{5}^{3}$+…+C${\;}_{10}^{3}$=（${C}_{4}^{4}$+${C}_{4}^{3}$）+${C}_{5}^{3}$+…+${C}_{10}^{3}$-1
    =${C}_{5}^{4}$+${C}_{5}^{3}$+…+${C}_{10}^{3}$-1
    =${C}_{6}^{4}$+…+${C}_{10}^{3}$-1
    =${C}_{10}^{4}$+${C}_{10}^{3}$-1
    =${C}_{11}^{4}$-1
    =329．
    故答案为：329．

    点评 本题考查了组合数公式的应用问题，也考查了公式灵活应用的问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．不论m为何实数，直线mx-y+3=0恒过定点（0，3）（填点的坐标）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1，F2，过右焦点F2作x轴的垂线，交椭圆于A，B两点．若等边△ABF1的周长为$4\sqrt{3}$，则椭圆的方程为（　　）
    A．$\frac{x^2}{3}+\frac{y^2}{2}=1$B．$\frac{x^2}{3}+\frac{y^2}{6}=1$C．$\frac{x^2}{2}+\frac{y^2}{3}=1$D．$\frac{x^2}{9}+\frac{y^2}{4}=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．若函数f（x）是定义在R上的偶函数，在区间（-∞，0）上是减函数，则使f（lnx）＜f（1）的x的取值范围为（$\frac{1}{e}$，e）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．求cos$\frac{8π}{3}$-tan$\frac{17π}{4}$+2sin（-$\frac{13π}{3}$）+tan（-$\frac{11π}{3}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．（xn）′=nxn-1；  
    （cosx）′=-sinx；    
    （ex）′=ex；
    （logax）′=$\frac{1}{xlna}$； 
    （ax）′=axlna．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．函数y=sin2x+cos2x的值域是（　　）
    A．[-1，1]B．[-2，2]C．[-1，$\sqrt{2}$]D．[-$\sqrt{2}$，$\sqrt{2}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．求函数f（x）=2x3-3x2-12x+5在区间[-2，3]上的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

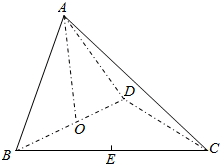    7．如图，在三棱锥A-BCD中，O，E分别是BD，BC的中点，CA=CB=CD=BD=2，AB=AD=$\sqrt{2}$．
    （1）求证：AO⊥平面BCD；
    （2）求三棱锥A-BCD体积．

    查看答案和解析>>

    同步练习册答案