Question

2．设数列{a_n}的前n项和为S_n，a₁=1，a₂=3，a₃=5且（2n+1）S_n+1-（2n+5）S_n=An+B，n∈N^*，其中A，a为常数．
（1）求A，B的值；
（2）证明：数列{a_n}为等差数列；
（3）数列{a_n}中是否存在两项a_m，a_k（m，k∈N^*），使得a_k⁴-2a_k+22=a_m^2_，若存在，求出所有的k和m，如果不存在，请说明理由．

Answer 1

分析 （1）由a₁=1，a₂=3，a₃=5且（2n+1）S_n+1-（2n+5）S_n=An+B，n∈N^*，分别取n=1，2，解出即可．
（2）由（1）可得：（2n+1）S_n+1-（2n+5）S_n=4n+1，化为（2n+1）a_n+1-4S_n=4n+1，当n≥2时，（2n-1）a_n-4S_n-1=4n-3，相减可得：（2n+1）a_n+1-（2n+3）a_n=4，再利用递推关系即可证明．
（3）由（2）可得：a_n=1+2（n-1）=2n-1．假设存在正整数k，m，使得a_k⁴-2a_k+22=a_m²成立，可得：（2k-1）⁴-2（2k-1）+22=（2m-1）²，由几何画板分别画出y=x⁴-2x+22，y=x²的图象，即可得出．

解答 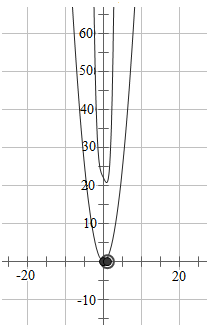（1）解：∵a₁=1，a₂=3，a₃=5且（2n+1）S_n+1-（2n+5）S_n=An+B，n∈N^*，
∴3×（1+3）-7=A+B，5×（1+3+5）-9×（1+3）=2A+B，
联立解得A=4，B=1．
（2）证明：由（1）可得：（2n+1）S_n+1-（2n+5）S_n=4n+1，
∴（2n+1）a_n+1-4S_n=4n+1，
当n≥2时，（2n-1）a_n-4S_n-1=4n-3，
相减可得：（2n+1）a_n+1-（2n+3）a_n=4，
∴（2n-1）a_n-（2n+1）a_n-1=4，
相减可得：（2n+1）a_n+1-（4n+2）a_n+（2n+1）a_n-1=0，
化为a_n+1+a_n-1=2a_n，
∴数列{a_n}为等差数列，首项为1，公差为2．
（3）解：由（2）可得：a_n=1+2（n-1）=2n-1．
假设存在正整数k，m，使得a_k⁴-2a_k+22=a_m²成立，
∴（2k-1）⁴-2（2k-1）+22=（2m-1）²，
由几何画板分别画出y=x⁴-2x+22，y=x²的图象，可知：两个图象无交点，
因此假设不成立，即不存在正整数k，m，使得a_k⁴-2a_k+22=a_m²成立．

点评 本题考查了等差数列的定义及其通项公式、递推关系的应用、函数的图象，考查了数形结合思想方法、推理能力与计算能力，属于中档题．