
ΓΨΧβΡΩΓΩΚ· ΐ ![]() ΆΦœσ…œ≤ΜΆ§ΝΫΒψ
ΆΦœσ…œ≤ΜΆ§ΝΫΒψ ![]() Θ§
Θ§ ![]() ¥Π«–œΏΒΡ–±¬ Ζ÷±π «
¥Π«–œΏΒΡ–±¬ Ζ÷±π « ![]() Θ§
Θ§ ![]() Θ§ΙφΕ®
Θ§ΙφΕ® ![]() Θ®
Θ® ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ ![]() ΒΡ≥ΛΕ»Θ©Ϋ–Ήω«ζœΏ
ΒΡ≥ΛΕ»Θ©Ϋ–Ήω«ζœΏ ![]() ‘ΎΒψ
‘ΎΒψ ![]() ”κ
”κ ![]() ÷°ΦδΒΡΓΑΆδ«ζΕ»Γ±Θ§Ηχ≥ω“‘œ¬ΟϋΧβΘΚ
÷°ΦδΒΡΓΑΆδ«ζΕ»Γ±Θ§Ηχ≥ω“‘œ¬ΟϋΧβΘΚ
ΔΌΚ· ΐ ![]() ΆΦœσ…œΝΫΒψ
ΆΦœσ…œΝΫΒψ ![]() ”κ
”κ ![]() ΒΡΚαΉχ±ξΖ÷±πΈΣ1ΚΆ2Θ§‘ρ
ΒΡΚαΉχ±ξΖ÷±πΈΣ1ΚΆ2Θ§‘ρ ![]() ΘΜ
ΘΜ
ΔΎ¥φ‘Ύ’β―υΒΡΚ· ΐΘ§ΆΦœσ…œ»Έ“βΝΫΒψ÷°ΦδΒΡΓΑΆδ«ζΕ»Γ±ΈΣ≥Θ ΐΘΜ
Δέ…ηΒψ ![]() Θ§
Θ§ ![]() «≈ΉΈοœΏ
«≈ΉΈοœΏ ![]() …œ≤ΜΆ§ΒΡΝΫΒψΘ§‘ρ
…œ≤ΜΆ§ΒΡΝΫΒψΘ§‘ρ ![]() ΘΜ
ΘΜ
Δή…η«ζœΏ ![]() Θ®
Θ® ![]() «Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©…œ≤ΜΆ§ΝΫΒψ
«Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©…œ≤ΜΆ§ΝΫΒψ ![]() Θ§
Θ§ ![]() Θ§«“
Θ§«“ ![]() Θ§»τ
Θ§»τ ![]() Κψ≥…ΝΔΘ§‘ρ Β ΐ
Κψ≥…ΝΔΘ§‘ρ Β ΐ ![]() ΒΡ»Γ÷ΒΖΕΈß «
ΒΡ»Γ÷ΒΖΕΈß « ![]() Θ°
Θ°
Τδ÷–’φΟϋΧβΒΡ–ρΚ≈ΈΣΘ®ΫΪΥυ”–’φΟϋΧβΒΡ–ρΚ≈ΕΦΧν…œΘ©
ΓΨ¥πΑΗΓΩΔΎΔέ
ΓΨΫβΈωΓΩΫβΘΚΕ‘”ΎΔΌΘ§”… ![]() ΒΟ
ΒΟ ![]() Θ§
Θ§
Ι ![]() Θ§
Θ§
”÷ ![]() Θ§Ι
Θ§Ι ![]() ΓΘ
ΓΘ
Γύ ![]() ΓΘΙ ΔΌ¥μΈσΓΘ
ΓΘΙ ΔΌ¥μΈσΓΘ
Ε‘”ΎΔΎΘ§≥Θ ΐΚ· ΐy=1¬ζΉψΆΦœσ…œ»Έ“βΝΫΒψ÷°ΦδΒΡΓΑΆδ«ζΕ»Γ±ΈΣ≥Θ ΐΘ§Ι ΔΎ’ΐ»ΖΘΜ
Ε‘”ΎΔέΘ§…η ![]() Θ§
Θ§ ![]() Θ§”÷
Θ§”÷ ![]() Θ§
Θ§
Γύ ![]()
![]() Θ§
Θ§
Γύ ![]() Θ§Ι Δέ’ΐ»ΖΓΘ
Θ§Ι Δέ’ΐ»ΖΓΘ
Ε‘”ΎΔήΘ§”… ![]() Ω…ΒΟ
Ω…ΒΟ ![]() Θ§
Θ§ 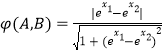 Θ§
Θ§
”… ![]() Κψ≥…ΝΔΩ…ΒΟ
Κψ≥…ΝΔΩ…ΒΟ ![]() Κψ≥…ΝΔΘ§
Κψ≥…ΝΔΘ§
ΕχΒ± ![]() ±ΗΟ ΫΚψ≥…ΝΔΘ§Ι Δή¥μΈσΓΘ
±ΗΟ ΫΚψ≥…ΝΔΘ§Ι Δή¥μΈσΓΘ
Ήέ…œΩ…ΒΟΔΎΔέ’ΐ»ΖΓΘ
Ι ¥πΑΗΈΣΘΚΔΎΔέ
±ΨΧβ÷ς“ΣΩΦ≤ιΚ· ΐΒΡΆΦœώΓΔ≈ΉΈοœΏΒΡΦρΒΞ–‘÷ ΦΑΚ· ΐΒΡ»Γ÷ΒΖΕΈßΓΘ



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑΜνΥ°ΈßΆχΓ±―χ”ψΦΦ θΨΏ”–―χ÷≥ΟήΕ»ΗΏΓΔΨ≠ΦΟ–ß“φΚΟΒΡΧΊΒψΘ°―–ΨΩ±μΟςΘΚΓΑΜνΥ°ΈßΆχΓ±―χ”ψ ±Θ§Ρ≥÷÷”ψ‘Ύ“ΜΕ®ΒΡΧθΦΰœ¬Θ§ΟΩΈ≤”ψΒΡΤΫΨυ…ζ≥ΛΥΌΕ»v(ΒΞΈΜΘΚ«ßΩΥ/Ρξ) «―χ÷≥ΟήΕ»x(ΒΞΈΜΘΚΈ≤/ΝΔΖΫΟΉ)ΒΡΚ· ΐΘ°Β±x≤Μ≥§Ιΐ4Έ≤/ΝΔΖΫΟΉ ±Θ§vΒΡ÷ΒΈΣ2«ßΩΥ/ΡξΘΜΒ±4<xΓή20 ±Θ§v «xΒΡ“Μ¥ΈΚ· ΐΘ§Β±x¥οΒΫ20Έ≤/ΝΔΖΫΟΉ ±Θ§“ρ»±―θΒ»‘≠“ρΘ§vΒΡ÷ΒΈΣ0«ßΩΥ/ΡξΘ°
Θ®1Θ©Β±0<xΓή20 ±Θ§«σΚ· ΐvΙΊ”ΎxΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©Β±―χ÷≥ΟήΕ»xΈΣΕύ¥σ ±Θ§”ψΒΡΡξ…ζ≥ΛΝΩ(ΒΞΈΜΘΚ«ßΩΥ/ΝΔΖΫΟΉ)Ω…“‘¥οΒΫΉν¥σΘΩ≤Δ«σ≥ωΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΚ· ΐfΘ®xΘ©=lnΘ®x2©¹2x©¹8Θ©ΒΡΒΞΒςΒί‘ω«χΦδ «Θ® Θ©
A.Θ®©¹ΓόΘ§©¹2Θ©
B.Θ®©¹ΓόΘ§©¹1Θ©
C.Θ®1Θ§+ΓόΘ©
D.Θ®4Θ§+ΓόΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η≈ΉΈοœΏy2=4xΒΡΫΙΒψΈΣFΘ§ΙΐΒψFΉς÷±œΏl”κ≈ΉΈοœΏΖ÷±πΫΜ”ΎΝΫΒψAΘ§BΘ§»τΒψM¬ζΉψ ![]() =
= ![]() Θ®
Θ® ![]() +
+ ![]() Θ©Θ§ΙΐMΉςy÷αΒΡ¥ΙœΏ”κ≈ΉΈοœΏΫΜ”ΎΒψPΘ§»τ|PF|=2Θ§‘ρMΒψΒΡΚαΉχ±ξΈΣ Θ°
Θ©Θ§ΙΐMΉςy÷αΒΡ¥ΙœΏ”κ≈ΉΈοœΏΫΜ”ΎΒψPΘ§»τ|PF|=2Θ§‘ρMΒψΒΡΚαΉχ±ξΈΣ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΦ·ΚœA={x|xΘΦ1}Θ§B={x|3xΘΦ1}Θ§‘ρΘ®ΓΓΓΓΘ©
A.AΓ…B={x|xΘΦ0}
B.AΓ»B=R
C.AΓ»B={x|xΘΨ1}
D.AΓ…B=
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΕ®“ε‘Ύ ![]() …œΒΡΚ· ΐ
…œΒΡΚ· ΐ ![]()
![]() Θ§«“
Θ§«“ ![]() Κψ≥…ΝΔ.
Κψ≥…ΝΔ.
Θ®1Θ©«σ Β ΐ ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©»τ ![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4-4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ ![]() ÷–Θ§‘≤
÷–Θ§‘≤ ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ ![]() Θ®
Θ® ![]() ΈΣ≤Έ ΐΘ§
ΈΣ≤Έ ΐΘ§ ![]() «¥σ”Ύ0ΒΡ≥Θ ΐΘ©Θ°“‘Ήχ±ξ‘≠ΒψΈΣΦΪΒψΘ§
«¥σ”Ύ0ΒΡ≥Θ ΐΘ©Θ°“‘Ήχ±ξ‘≠ΒψΈΣΦΪΒψΘ§ ![]() ÷α’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§‘≤
÷α’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§‘≤ ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ ![]() Θ°
Θ°
Θ®1Θ©«σ‘≤ ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΚΆ‘≤
ΒΡΦΪΉχ±ξΖΫ≥ΧΚΆ‘≤ ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©Ζ÷±πΦ«÷±œΏ ![]() ΘΚ
ΘΚ ![]() Θ§
Θ§ ![]() ”κ‘≤
”κ‘≤ ![]() ΓΔ‘≤
ΓΔ‘≤ ![]() ΒΡ“λ”Ύ‘≠ΒψΒΡΫΙΒψΈΣ
ΒΡ“λ”Ύ‘≠ΒψΒΡΫΙΒψΈΣ ![]() Θ§
Θ§ ![]() Θ§»τ‘≤
Θ§»τ‘≤ ![]() ”κ‘≤
”κ‘≤ ![]() Άβ«–Θ§ ‘«σ Β ΐ
Άβ«–Θ§ ‘«σ Β ΐ ![]() ΒΡ÷ΒΦΑœΏΕΈ
ΒΡ÷ΒΦΑœΏΕΈ ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ÷±»ΐάβ÷υ ![]() ÷–Θ§
÷–Θ§ ![]() ΈΣ±Ώ≥ΛΈΣ2ΒΡΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣ±Ώ≥ΛΈΣ2ΒΡΒ»±Ώ»ΐΫ«–ΈΘ§ ![]() Θ§Βψ
Θ§Βψ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() Ζ÷±π «±Ώ
Ζ÷±π «±Ώ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() ΒΡ÷–ΒψΘ§Ε·Βψ
ΒΡ÷–ΒψΘ§Ε·Βψ ![]() ‘ΎΥΡ±Ώ–Έ
‘ΎΥΡ±Ώ–Έ ![]() ΡΎ≤Ω‘ΥΕ·Θ§≤Δ«“ Φ÷’”–
ΡΎ≤Ω‘ΥΕ·Θ§≤Δ«“ Φ÷’”– ![]() ΤΫΟφ
ΤΫΟφ ![]() Θ§‘ρΕ·Βψ
Θ§‘ρΕ·Βψ ![]() ΒΡΙλΦΘ≥ΛΕ»ΈΣΘ® Θ©
ΒΡΙλΦΘ≥ΛΕ»ΈΣΘ® Θ©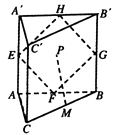
A.![]()
B.![]()
C.![]()
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫϋΡξά¥ΥφΉ≈Έ“Ιζ‘ΎΫΧ”ΐάϊ―–…œΒΡΆΕ»κ≤ΜΕœΦ”¥σΘ§ΩΤ―ßΦΦ θΒΟΒΫ―ΗΟΆΖΔ’ΙΘ§ΙζΡΎΤσ“ΒΒΡΙζΦ ΨΚ’υΝΠΒΟΒΫ¥σΖυΧα…ΐ.ΑιΥφΉ≈ΙζΡΎ –≥Γ‘ωΥΌΖ≈ΜΚΘ§ΙζΡΎ»Ζ ΒΝΠΤσ“ΒΖΉΖΉΫχ––ΚΘΆβ≤ΦΨ÷Θ§ΒΎΕΰ¬÷Τσ“Β≥ωΚΘ≥±ΒΫά¥Θ§»γ‘Ύ÷«Ρή ÷Μζ––“ΒΘ§Ιζ≤ζΤΖ≈Τ“―‘ΎΗœ≥§ΙζΆβΨόΆΖΘ§Ρ≥ΤΖ≈Τ ÷ΜζΙΪΥΨ“Μ÷±Ρ§Ρ§ΆΊ’ΙΚΘΆβ –≥ΓΘ§‘ΎΚΘΆβΙ≤…η30ΕύΗωΖ÷÷ßΜζΙΙΘ§–η“ΣΙζΡΎΙΪΥΨΆβ≈…¥σΝΩ70ΚσΓΔ80Κσ÷–«ύΡξ‘±ΙΛΘ°ΗΟΤσ“ΒΈΣΝΥΫβ’βΝΫΗωΡξΝδ≤ψ‘±ΙΛ «Ζώ‘Η“β±ΜΆβ≈……œΉςΒΡΧ§Ε»Θ§Α¥Ζ÷≤ψ≥ι―υΒΡΖΫ Ϋ¥”70Κσάϊ80ΚσΒΡ‘±ΙΛ÷–ΥφΜζΒς≤ιΝΥ100ΈΜΘ§ΒΟΒΫ ΐΨί»γœ¬±μΘΚ
‘Η“β±ΜΆβ≈… | ≤Μ‘Η“β±ΜΆβ≈… | ΚœΦΤ | |
70Κσ | 20 | 20 | 40 |
80Κσ | 40 | 20 | 60 |
ΚœΦΤ | 60 | 40 | 100 |
≤ΈΩΦ ΐΨίΘΚ
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
Θ®≤ΈΩΦΙΪ ΫΘΚ ![]() Θ§Τδ÷–
Θ§Τδ÷– ![]() Θ©
Θ©
Θ®1Θ©ΗυΨί≤ιΒΡ ΐΨίΘ§ «Ζώ”– ![]() ΒΡΑ―Έ’»œΈΣΓΑ «Ζώ‘Η“β±ΜΆβ≈…”κΡξΝδ”–ΙΊΓ±Θ§≤ΔΥΒΟςάμ”…ΘΜ
ΒΡΑ―Έ’»œΈΣΓΑ «Ζώ‘Η“β±ΜΆβ≈…”κΡξΝδ”–ΙΊΓ±Θ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©ΗΟΙΪΥΨ≤ΈΙέΉΛΚΘΆβΖ÷÷ßΜζΙΙΒΡΫΜΝςΧε―ιΜνΕ·Θ§ΡβΑ≤≈≈4Οϊ≤Έ”κΒς≤ιΒΡ70Κσ‘±ΙΛ≤ΈΦ”Θ§70ΚσΒΡ‘±ΙΛ÷–”–‘Η“β±ΜΆβ≈…ΒΡ3»ΥΚΆ≤Μ‘Η“β±ΜΆβ≈…ΒΡ3»Υ±®Οϊ≤ΈΦ”Θ§œ÷≤…”ΟΥφΜζ≥ι―υΖΫΖ®¥”±®ΟϊΒΡ‘±ΙΛ÷–―Γ4»ΥΘ§«σ―ΓΒΫ‘Η“β±ΜΆβ≈…»Υ ΐ≤Μ…Ό”Ύ≤Μ‘Η“β±ΜΆβ≈…»Υ ΐΒΡΗ≈¬ .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com