
【题目】近年来随着我国在教育利研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内确实力企业纷纷进行海外布局,第二轮企业出海潮到来,如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设30多个分支机构,需要国内公司外派大量70后、80后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派上作的态度,按分层抽样的方式从70后利80后的员工中随机调查了100位,得到数据如下表:
愿意被外派 | 不愿意被外派 | 合计 | |
70后 | 20 | 20 | 40 |
80后 | 40 | 20 | 60 |
合计 | 60 | 40 | 100 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(参考公式: ![]() ,其中
,其中 ![]() )
)
(1)根据查的数据,是否有 ![]() 的把握认为“是否愿意被外派与年龄有关”,并说明理由;
的把握认为“是否愿意被外派与年龄有关”,并说明理由;
(2)该公司参观驻海外分支机构的交流体验活动,拟安排4名参与调查的70后员工参加,70后的员工中有愿意被外派的3人和不愿意被外派的3人报名参加,现采用随机抽样方法从报名的员工中选4人,求选到愿意被外派人数不少于不愿意被外派人数的概率.
【答案】
(1)解: ![]()
![]() 所以有
所以有 ![]() 以上的把握认为“是否愿意被外派与年龄有关”
以上的把握认为“是否愿意被外派与年龄有关”
(2)解:设 ![]() 后员工中报名参加活动有愿意被外派的
后员工中报名参加活动有愿意被外派的 ![]() 人为
人为 ![]() ,不愿意被外派的
,不愿意被外派的 ![]() 人为
人为 ![]() ,现从中选
,现从中选 ![]() 人,如图表所示,用
人,如图表所示,用 ![]() 表示没有被选到,
表示没有被选到,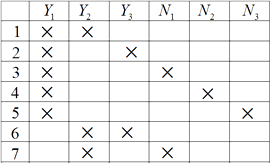
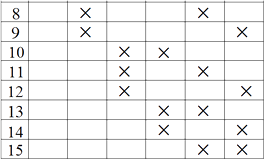
(可以以不同形式列举出15种情况)
则“愿意被外派人数不少于不愿意被外派人数”即“愿意被外派人数为 ![]() 人或
人或 ![]() 人”
人”
共 ![]() 种情况,则其概率
种情况,则其概率 ![]()
【解析】(1)本题考查独立性检验,首先在![]() 列联表中找到a,b,c,d,n,然后代入 K2 , 求解后与k作比较,即可得出答案。
列联表中找到a,b,c,d,n,然后代入 K2 , 求解后与k作比较,即可得出答案。
(2)本题考查简单随机抽样,确定总体是从6个人中抽出4人,样本是要求愿意的人数大于等于不愿意的人数,分为愿意和不愿意都抽2人;愿意抽3人,不愿意抽1人,这两种情况。


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】函数 ![]() 图象上不同两点
图象上不同两点 ![]() ,
, ![]() 处切线的斜率分别是
处切线的斜率分别是 ![]() ,
, ![]() ,规定
,规定 ![]() (
( ![]() 为线段
为线段 ![]() 的长度)叫做曲线
的长度)叫做曲线 ![]() 在点
在点 ![]() 与
与 ![]() 之间的“弯曲度”,给出以下命题:
之间的“弯曲度”,给出以下命题:
①函数 ![]() 图象上两点
图象上两点 ![]() 与
与 ![]() 的横坐标分别为1和2,则
的横坐标分别为1和2,则 ![]() ;
;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点 ![]() ,
, ![]() 是抛物线
是抛物线 ![]() 上不同的两点,则
上不同的两点,则 ![]() ;
;
④设曲线 ![]() (
( ![]() 是自然对数的底数)上不同两点
是自然对数的底数)上不同两点 ![]() ,
, ![]() ,且
,且 ![]() ,若
,若 ![]() 恒成立,则实数
恒成立,则实数 ![]() 的取值范围是
的取值范围是 ![]() .
.
其中真命题的序号为(将所有真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有下面四个命题
p1:若复数z满足 ![]() ∈R,则z∈R;
∈R,则z∈R;
p2:若复数z满足z2∈R,则z∈R;
p3:若复数z1 , z2满足z1z2∈R,则z1= ![]() ;
;
p4:若复数z∈R,则 ![]() ∈R.
∈R.
其中的真命题为( )
A.p1 , p3
B.p1 , p4
C.p2 , p3
D.p2 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=2x2-ln x在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
A.[1,+∞)
B.[1,2)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln x-bx2 , a,b∈R.
(1)若f(x)在x=1处与直线y=- ![]() 相切,求a,b的值;
相切,求a,b的值;
(2)在(1)的条件下,求f(x)在 ![]() 上的最大值;
上的最大值;
(3)若不等式f(x)≥x对所有的b∈(-∞,0],x∈(e,e2]都成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() :
: ![]() (
( ![]() )的焦距与椭圆
)的焦距与椭圆 ![]() :
: ![]() 的短轴长相等,且
的短轴长相等,且 ![]() 与
与 ![]() 的长轴长相等,这两个椭圆在第一象限的交点为
的长轴长相等,这两个椭圆在第一象限的交点为 ![]() ,直线
,直线 ![]() 经过
经过 ![]() 在
在 ![]() 轴正半轴上的顶点
轴正半轴上的顶点 ![]() 且与直线
且与直线 ![]() (
( ![]() 为坐标原点)垂直,
为坐标原点)垂直, ![]() 与
与 ![]() 的另一个交点为
的另一个交点为 ![]() ,
, ![]() 与
与 ![]() 交于
交于 ![]() ,
, ![]() 两点.
两点.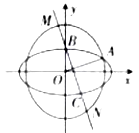
(1)求 ![]() 的标准方程;
的标准方程;
(2)求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为半圆
为半圆 ![]() 的直径,点
的直径,点 ![]() 是半圆弧上的两点,
是半圆弧上的两点, ![]() ,
, ![]() .曲线
.曲线 ![]() 经过点
经过点 ![]() ,且曲线
,且曲线 ![]() 上任意点
上任意点 ![]() 满足:
满足: ![]() 为定值.
为定值.
(Ⅰ)求曲线 ![]() 的方程;
的方程;
(Ⅱ)设过点 ![]() 的直线
的直线 ![]() 与曲线
与曲线 ![]() 交于不同的两点
交于不同的两点 ![]() ,求
,求 ![]() 面积最大时的直线
面积最大时的直线 ![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com