
【题目】若函数f(x)=2x2-ln x在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
A.[1,+∞)
B.[1,2)
C.![]()
D.![]()
【答案】C
【解析】∵f(x)=2x2-lnx(x>0),
∴f′(x)=4x- ![]() =
= ![]() (x>0),
(x>0),
由f′(x)=0,得x= ![]() ,
,
当x∈(0, ![]() )时,f′(x)<0,f(x)单调递减;
)时,f′(x)<0,f(x)单调递减;
当x∈( ![]() ,+∞)时,f′(x)>0,f(x)单调递增.
,+∞)时,f′(x)>0,f(x)单调递增.
据题意, 
解得1≤k< ![]() .
.
故答案为:C.
先确定函数的定义域然后求导数fˊ(x),在函数的定义域内解方程fˊ(x)=0,使方程的解在定义域内的一个子区间(k-1,k+1)内,建立不等关系,解之即可.导数和函数的单调性的关系:
(1)若f′(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数,f′(x)>0的解集与定义域的交集的对应区间为增区间;
(2)若f′(x)<0在(a,b)上恒成立,则f(x)在(a,b)上是减函数,f′(x)<0的解集与定义域的交集的对应区间为减区间.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】设抛物线y2=4x的焦点为F,过点F作直线l与抛物线分别交于两点A,B,若点M满足 ![]() =
= ![]() (
( ![]() +
+ ![]() ),过M作y轴的垂线与抛物线交于点P,若|PF|=2,则M点的横坐标为 .
),过M作y轴的垂线与抛物线交于点P,若|PF|=2,则M点的横坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图直三棱柱 ![]() 中,
中, ![]() 为边长为2的等边三角形,
为边长为2的等边三角形, ![]() ,点
,点 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 分别是边
分别是边 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 的中点,动点
的中点,动点 ![]() 在四边形
在四边形 ![]() 内部运动,并且始终有
内部运动,并且始终有 ![]() 平面
平面 ![]() ,则动点
,则动点 ![]() 的轨迹长度为( )
的轨迹长度为( )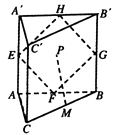
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且a>b,a>c.△ABC的外接圆半径为1, ![]() ,若边BC上一点D满足BD=2DC,且∠BAD=90°,则△ABC的面积为 .
,若边BC上一点D满足BD=2DC,且∠BAD=90°,则△ABC的面积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为半圆
为半圆 ![]() 的直径,点
的直径,点 ![]() 是半圆弧上的两点,
是半圆弧上的两点, ![]() ,
, ![]() .曲线
.曲线 ![]() 经过点
经过点 ![]() ,且曲线
,且曲线 ![]() 上任意点
上任意点 ![]() 满足:
满足: ![]() 为定值.
为定值.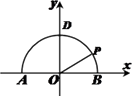
(Ⅰ)求曲线 ![]() 的方程;
的方程;
(Ⅱ)设过点 ![]() 的直线
的直线 ![]() 与曲线
与曲线 ![]() 交于不同的两点
交于不同的两点 ![]() ,求
,求 ![]() 面积最大时的直线
面积最大时的直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳a元(a为常数,2≤a≤5)的管理费,根据多年的统计经验,预计当每件产品的售价为x元时,产品一年的销售量为 ![]() (e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(1)求分公司经营该产品一年的利润L(x)万元与每件产品的售价x元的函数关系式;
(2)当每件产品的售价为多少元时,该产品一年的利润L(x)最大,并求出L(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来随着我国在教育利研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内确实力企业纷纷进行海外布局,第二轮企业出海潮到来,如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设30多个分支机构,需要国内公司外派大量70后、80后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派上作的态度,按分层抽样的方式从70后利80后的员工中随机调查了100位,得到数据如下表:
愿意被外派 | 不愿意被外派 | 合计 | |
70后 | 20 | 20 | 40 |
80后 | 40 | 20 | 60 |
合计 | 60 | 40 | 100 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(参考公式: ![]() ,其中
,其中 ![]() )
)
(1)根据查的数据,是否有 ![]() 的把握认为“是否愿意被外派与年龄有关”,并说明理由;
的把握认为“是否愿意被外派与年龄有关”,并说明理由;
(2)该公司参观驻海外分支机构的交流体验活动,拟安排4名参与调查的70后员工参加,70后的员工中有愿意被外派的3人和不愿意被外派的3人报名参加,现采用随机抽样方法从报名的员工中选4人,求选到愿意被外派人数不少于不愿意被外派人数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),点
为参数),点 ![]() 是曲线
是曲线 ![]() 上的一动点,以坐标原点为极点,
上的一动点,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 ![]() 的方程为
的方程为 ![]() .
.
(Ⅰ)求线段 ![]() 的中点
的中点 ![]() 的轨迹的极坐标方程;
的轨迹的极坐标方程;
(Ⅱ)求曲线 ![]() 上的点到直线
上的点到直线 ![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com