
【题目】已知函数f(x)=aln x-bx2 , a,b∈R.
(1)若f(x)在x=1处与直线y=- ![]() 相切,求a,b的值;
相切,求a,b的值;
(2)在(1)的条件下,求f(x)在 ![]() 上的最大值;
上的最大值;
(3)若不等式f(x)≥x对所有的b∈(-∞,0],x∈(e,e2]都成立,求a的取值范围.
【答案】
(1)解:f′(x)= ![]() -2bx.由函数f(x)在x=1处与直线y=-
-2bx.由函数f(x)在x=1处与直线y=- ![]() 相切,
相切,
得  即
即 
解得 ![]()
(2)解:由(1)得f(x)=ln x- ![]() x2 , 定义域为(0,+∞).
x2 , 定义域为(0,+∞).
此时,f′(x)= ![]() -x=
-x= ![]() ,令f′(x)>0,解得0<x<1,令f′(x)<0,解得x>1.
,令f′(x)>0,解得0<x<1,令f′(x)<0,解得x>1.
所以f′(x)在 ![]() 上单调递增,在(1,e)上单调递减,
上单调递增,在(1,e)上单调递减,
所以f(x)在 ![]() 上的最大值为f(1)=-
上的最大值为f(1)=- ![]() .
.
(3)解:若不等式f(x)≥x对所有的b∈(-∞,0],x∈(e,e2]都成立,
即aln x-bx2≥x对所有的b∈(-∞,0],x∈(e,e2]都成立,
即aln x-x≥bx2对所有的b∈(-∞,0],x∈(e,e2]都成立,
即aln x-x≥0对x∈(e,e2]恒成立,
即a≥ ![]() 对x∈(e,e2]恒成立,
对x∈(e,e2]恒成立,
即a大于等于 ![]() 在区间(e,e2]上的最大值.
在区间(e,e2]上的最大值.
令h(x)= ![]() ,则h′(x)=
,则h′(x)= ![]() ,当x∈(e,e2)时,h′(x)>0,h(x)单调递增,
,当x∈(e,e2)时,h′(x)>0,h(x)单调递增,
所以h(x)= ![]() ,x∈(e,e2]的最大值为h(e2)=
,x∈(e,e2]的最大值为h(e2)= ![]() ,即a≥
,即a≥ ![]() .
.
所以a的取值范围为 ![]() .
.
【解析】本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查不等式的恒成立问题注意运用参数分离和转化为求函数的最值问题,属于中档题和易错题.导数和函数的单调性的关系:
(1)若f′(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数,f′(x)>0的解集与定义域的交集的对应区间为增区间;
(2)若f′(x)<0在(a,b)上恒成立,则f(x)在(a,b)上是减函数,f′(x)<0的解集与定义域的交集的对应区间为减区间.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图, ![]() 为半圆
为半圆 ![]() 的直径,点
的直径,点 ![]() 是半圆弧上的两点,
是半圆弧上的两点, ![]() ,
, ![]() .曲线
.曲线 ![]() 经过点
经过点 ![]() ,且曲线
,且曲线 ![]() 上任意点
上任意点 ![]() 满足:
满足: ![]() 为定值.
为定值.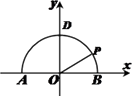
(Ⅰ)求曲线 ![]() 的方程;
的方程;
(Ⅱ)设过点 ![]() 的直线
的直线 ![]() 与曲线
与曲线 ![]() 交于不同的两点
交于不同的两点 ![]() ,求
,求 ![]() 面积最大时的直线
面积最大时的直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来随着我国在教育利研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内确实力企业纷纷进行海外布局,第二轮企业出海潮到来,如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设30多个分支机构,需要国内公司外派大量70后、80后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派上作的态度,按分层抽样的方式从70后利80后的员工中随机调查了100位,得到数据如下表:
愿意被外派 | 不愿意被外派 | 合计 | |
70后 | 20 | 20 | 40 |
80后 | 40 | 20 | 60 |
合计 | 60 | 40 | 100 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(参考公式: ![]() ,其中
,其中 ![]() )
)
(1)根据查的数据,是否有 ![]() 的把握认为“是否愿意被外派与年龄有关”,并说明理由;
的把握认为“是否愿意被外派与年龄有关”,并说明理由;
(2)该公司参观驻海外分支机构的交流体验活动,拟安排4名参与调查的70后员工参加,70后的员工中有愿意被外派的3人和不愿意被外派的3人报名参加,现采用随机抽样方法从报名的员工中选4人,求选到愿意被外派人数不少于不愿意被外派人数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),直线
为参数),直线 ![]() 的参数方程为
的参数方程为 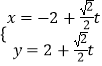 (
( ![]() 为参数).
为参数).
(Ⅰ)求曲线 ![]() 和直线
和直线 ![]() 的普通方程;
的普通方程;
(Ⅱ)若点 ![]() 为曲线
为曲线 ![]() 上一点,求点
上一点,求点 ![]() 到直线
到直线 ![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆 ![]() 与直线
与直线 ![]() 相切.
相切.
(1)若直线 ![]() 与圆
与圆 ![]() 交于
交于 ![]() 两点,求
两点,求 ![]() ;
;
(2)设圆 ![]() 与
与 ![]() 轴的负半轴的交点为
轴的负半轴的交点为 ![]() ,过点
,过点 ![]() 作两条斜率分别为
作两条斜率分别为 ![]() 的直线交圆
的直线交圆 ![]() 于
于 ![]() 两点,且
两点,且 ![]() ,试证明直线
,试证明直线 ![]() 恒过一定点,并求出该定点的坐标.
恒过一定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com