
【题目】已知 ![]() ,
, ![]() ,函数
,函数 ![]() 的最小值为4.
的最小值为4.
(1)求 ![]() 的值;
的值;
(2)求 ![]() 的最小值.
的最小值.
【答案】
(1)解:因为, ![]() ,
,
所以 ![]() ,当且仅当
,当且仅当 ![]() 时,等号成立,又
时,等号成立,又 ![]() ,
, ![]() ,
,
所以 ![]() ,所以
,所以 ![]() 的最小值为
的最小值为 ![]() ,所以
,所以 ![]() .
.
(2)解:由(1)知 ![]() ,
, ![]() .
.![]()
当且仅当 ![]() ,
, ![]() 时,
时, ![]() 的最小值为
的最小值为 ![]() .
.
【解析】(1)根据绝对值的性质,可得| x + a | + | x b | ≥ | a b | = | a + b | ,所以 ![]() ,当且仅当
,当且仅当 ![]() 时,等号成立,又
时,等号成立,又 ![]() ,
, ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() 的最小值为
的最小值为 ![]() ,所以
,所以 ![]() .
.
(2)因为 a + b = 4 , b = 4 a ,将b参数化掉最后变成一个一元二次方程,就可以求出其最小值.
【考点精析】解答此题的关键在于理解复合函数单调性的判断方法的相关知识,掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”,以及对二次函数在闭区间上的最值的理解,了解当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】编号为 ![]() 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12] | 31 | 38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
区间 |
|
|
|
人数 |
(Ⅱ)从得分在区间 ![]() 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数 ![]() ,
, ![]() ,对于给定的非零实数
,对于给定的非零实数 ![]() ,总存在非零常数
,总存在非零常数 ![]() ,使得定义域
,使得定义域 ![]() 内的任意实数
内的任意实数 ![]() ,都有
,都有 ![]() 恒成立,此时
恒成立,此时 ![]() 为
为 ![]() 的类周期,函数
的类周期,函数 ![]() 是
是 ![]() 上的
上的 ![]() 级类周期函数.若函数
级类周期函数.若函数 ![]() 是定义在区间
是定义在区间 ![]() 内的2级类周期函数,且
内的2级类周期函数,且 ![]() ,当
,当 ![]() 时,
时, 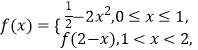 函数
函数 ![]() .若
.若 ![]() ,
, ![]() ,使
,使 ![]() 成立,则实数
成立,则实数 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
(1)若函数f(x)的图象过点(-2,1),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(2)在(1)的条件下,当x∈[-1,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,底面梯形
中,底面梯形 ![]() ,
, ![]() ,平面
,平面 ![]() 平面
平面 ![]() ,
, ![]() 是等边三角形,已知
是等边三角形,已知 ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 上任意一点,
上任意一点, ![]() ,且
,且 ![]() .
.
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)试确定 ![]() 的值,使三棱锥
的值,使三棱锥 ![]() 体积为三棱锥
体积为三棱锥 ![]() 体积的3倍.
体积的3倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有下面四个命题
p1:若复数z满足 ![]() ∈R,则z∈R;
∈R,则z∈R;
p2:若复数z满足z2∈R,则z∈R;
p3:若复数z1 , z2满足z1z2∈R,则z1= ![]() ;
;
p4:若复数z∈R,则 ![]() ∈R.
∈R.
其中的真命题为( )
A.p1 , p3
B.p1 , p4
C.p2 , p3
D.p2 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C的对边分别a,b,c,已知 ![]() ,
, ![]() ,且
,且 ![]() ∥
∥ ![]()
(1)证明sinBsinC=sinA;
(2)若a2+c2﹣b2= ![]() ac,求tanC.
ac,求tanC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln x-bx2 , a,b∈R.
(1)若f(x)在x=1处与直线y=- ![]() 相切,求a,b的值;
相切,求a,b的值;
(2)在(1)的条件下,求f(x)在 ![]() 上的最大值;
上的最大值;
(3)若不等式f(x)≥x对所有的b∈(-∞,0],x∈(e,e2]都成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com