
【题目】连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号,某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传,要求版心面积为162 ![]() (版心是指图中的长方形阴影部分,
(版心是指图中的长方形阴影部分,![]() 为长度单位分米),上、下两边各空2
为长度单位分米),上、下两边各空2 ![]() ,左、右两边各空1
,左、右两边各空1 ![]() .
.

(Ⅰ)若设版心的高为![]()
![]() ,求海报四周空白面积关于
,求海报四周空白面积关于![]() 的函数
的函数![]() 的解析式;
的解析式;
(Ⅱ)要使海报四周空白面积最小,版心的高和宽该如何设计?
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】设数据![]() 是郑州市普通职工
是郑州市普通职工![]() 个人的年收入,若这
个人的年收入,若这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A. 年收入平均数大大增大,中位数一定变大,方差可能不变
B. 年收入平均数大大增大,中位数可能不变,方差变大
C. 年收入平均数大大增大,中位数可能不变,方差也不变
D. 年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面是边长为1的正方形,侧棱PD=1,PA=PC=![]() .
.
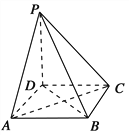
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象上有一点列
的图象上有一点列![]() ,点
,点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() (
(![]() 且
且![]() ),
), ![]() .
.
(1)求证: ![]() 是等比数列,并求出数列
是等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设四边形![]() 的面积是
的面积是![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路.记两条相互垂直的公路为![]() ,山区边界曲线为
,山区边界曲线为![]() .计划修建的公路为
.计划修建的公路为![]() ,如图所示,
,如图所示,![]() 为
为![]() 的两个端点,测得点
的两个端点,测得点![]() 到
到![]() 的距离分别为5千米和40千米,点
的距离分别为5千米和40千米,点![]() 到
到![]() 的距离分别为20千米和2.5千米,以
的距离分别为20千米和2.5千米,以![]() 所在直线分别为
所在直线分别为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() .假设曲线
.假设曲线![]() 符合函数
符合函数![]() (其中
(其中![]() 为常数)模型.
为常数)模型.
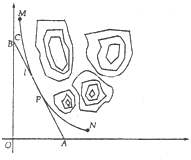
(1)求![]() 的值;
的值;
(2)设公路![]() 与曲线
与曲线![]() 相切于
相切于![]() 点,
点,![]() 的横坐标为
的横坐标为![]() .
.
①请写出公路![]() 长度的函数解析式
长度的函数解析式![]() ,并写出其定义域;
,并写出其定义域;
②当![]() 为何值时,公路
为何值时,公路![]() 的长度最短?求出最短长度.
的长度最短?求出最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 是直线
是直线![]() 上的一动点,过点
上的一动点,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() .
.
(1)当切线![]() 的长度为
的长度为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)若![]() 的外接圆为圆
的外接圆为圆![]() ,试问:当
,试问:当![]() 在直线
在直线![]() 上运动时,圆
上运动时,圆![]() 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有学生 ![]() 人,其中一年级
人,其中一年级 ![]() 人,二、三年级各
人,二、三年级各 ![]() 人,现要用抽样方法抽取
人,现要用抽样方法抽取 ![]() 人形成样本,将学生按一、二、三年级依次统一编号为
人形成样本,将学生按一、二、三年级依次统一编号为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,如果抽得号码有下列四种情况:
,如果抽得号码有下列四种情况:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
②![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
③![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
④![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
其中可能是由分层抽样得到,而不可能是由系统抽样得到的一组号码为 ![]()
A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com