
分析 (Ⅰ)求出${f}^{'}(x)=\frac{1}{{x}^{2}}[(x-1)({e}^{x}-a)]$,根据0<a≤1,1<a<e,a=e,a>e进行分类讨论,利用导数性质能讨论f(x)的单调性.
(Ⅱ)0<g(x)<1等价于1+xlnx>0,且$lnx<\frac{{{e^x}-1}}{x}$,由此利用导数性质能证明0<g(x)<1.
解答 解:(Ⅰ)$f'(x)=\frac{{{e^x}x-({{e^x}-a})}}{x^2}-\frac{a}{x}$=$\frac{{({x-1}){e^x}+a}}{x^2}-\frac{ax}{x^2}$
=$\frac{1}{x^2}[{({x-1}){e^x}+a-ax}]$=$\frac{1}{x^2}[{({x-1})({{e^x}-a})}]$
(1)当0<a≤1时,ex>a,当x∈(0,1),f'(x)<0;当x∈(1,+∞),f'(x)>0;
所以f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
(2)当1<a<e时,令ex=a,得x=lna∈(0,1),
由f'(x)<0得lna<x<1,由f'(x)>0得0<x<lna或x>lna,
所以f(x)在(0,lna),(1,+∞)上单调递增,在(lna,1)上单调递减.
(3)当a=e时,令ex=a,f'(x)≥0,故f(x)在(0,+∞)上递增.
(4)当a>e时,令ex=a,得x=lna∈(1,+∞),
由f'(x)<0得1<x<lna,由f'(x)>0得0<x<1或x>lna,
所以f(x)在(0,1),(lna,+∞)上单调递增,在(1,lna)上单调递减.
综上,当0<a≤1时,f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
当1<a<e时,f(x)在(0,lna),(1,+∞)上单调递增,在(lna,1)上单调递减.
当a=e时,f(x)在(0,+∞)上递增.
当a>e时,f(x)在(0,1),(lna,+∞)上单调递增,在(1,lna)上单调递减.
证明:(Ⅱ)0<g(x)<1?$0<\frac{1+xlnx}{e^x}<1?$1+xlnx>0①且$lnx<\frac{{{e^x}-1}}{x}$②
先证①:令h(x)=1+xlnx,则h(x)=1+lnx,
当$x∈({0,\frac{1}{e}})$,h'(x)<0,h(x)单调递减;当$x∈({\frac{1}{e},+∞})$,h'(x)>0,h(x)单调递增;
所以$h(x)≥h({\frac{1}{e}})$=$1+\frac{1}{e}ln\frac{1}{e}$=$1-\frac{1}{e}>0$,故①成立!
再证②:由(Ⅰ),当a=1时,$f(x)=\frac{{{e^x}-1}}{x}-lnx$在(0,1)上单调递减,在(1,+∞)上单调递增,
所以f(x)≥f(1)=e-1>0,故②成立!
综上,0<g(x)<1恒成立.
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).| 工种类别 | A | B | C |
| 赔付频率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
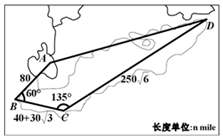 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,$BC=40+30\sqrt{3}$nmile,$CD=250\sqrt{6}$nmile.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,则收到指令时该轮船到城市C的距离是100nmile.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,$BC=40+30\sqrt{3}$nmile,$CD=250\sqrt{6}$nmile.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,则收到指令时该轮船到城市C的距离是100nmile.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 75%,170 | B. | 75%,340 | C. | 25%,170 | D. | 25%,340 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com