
设集合A={1,2,a},B={x|-1<x<2a-1},A∩B=A,则实数a的取值范围是( )
A.(1,+∞) B.( ,+∞)
,+∞)
C.(1,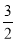 ) D.(
) D.( ,2)∪(2,+∞)
,2)∪(2,+∞)
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-5古典概型(解析版) 题型:选择题
从0,1,2,3,4,5这6个数字中任意取4个数字组成一个没有重复数字的四位数,这个数不能被3整除的概率为( )
A.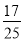 B.
B.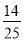 C.
C. D.
D.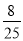
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-2排列与组合(解析版) 题型:解答题
有3名男生,4名女生,在下列不同要求下,求不同的排列方法总数:
(1)选其中5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体排成一排,甲不站在排头也不站在排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻;
(6)全体排成一排,甲、乙两人中间恰好有3人.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:解答题
有六名同学报名参加三个智力竞赛项目,在下列情况下各有多少种不同的报名方法?(不一定六名同学都能参加)
(1)每人恰好参加一项,每项人数不限;
(2)每项限报一人,且每人至多参加一项;
(3)每项限报一人,但每人参加的项目不限.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:填空题
某县从10名大学毕业的选调生中选3个人担任镇长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数为( )
A.85 B.56 C.49 D.28
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:1-1集合的概念与运算(解析版) 题型:填空题
若集合A={x|x2+2x-8<0},B={x|5-m<x<2m-1}.若U=R,A∩( ∁UB)=A,则实数m的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:1-1集合的概念与运算(解析版) 题型:选择题
已知集合A={y|y=(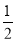 )x2+1,x∈R},则满足A∩B=B的集合B可以是( )
)x2+1,x∈R},则满足A∩B=B的集合B可以是( )
A.{0,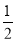 } B.{x|-1≤x≤1}
} B.{x|-1≤x≤1}
C.{x|0<x<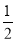 } D.{x|x>0}
} D.{x|x>0}
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练1(解析版) 题型:填空题
我们把形如y=f(x)φ(x)的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得ln y=φ(x)lnf(x),两边求导得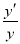 =φ′(x)·ln f(x)+φ(x)·
=φ′(x)·ln f(x)+φ(x)·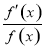 ,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·
,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·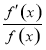 ].运用此方法可以探求得y=x
].运用此方法可以探求得y=x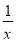 的单调递增区间是________.
的单调递增区间是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:6-3二元一次不等式及简单的线性规划(解析版) 题型:填空题
已知实数x,y满足 ,若目标函数z=ax+y(a≠0)取得最小值时的最优解有无数个,则实数a的值为________.
,若目标函数z=ax+y(a≠0)取得最小值时的最优解有无数个,则实数a的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com