
分析 (1)由题意设出椭圆方程,再由抛物线方程求出抛物线焦点坐标,可得椭圆的短半轴长,结合离心率及隐含条件求得a,则椭圆方程可求;
(2)由题意可设直线l的方程为y=k(x-2)+1 (k≠0),联立直线方程和椭圆方程,由判别式等于0求得k,进一步求得切点M的坐标;
(3)若存在直线l1满足条件,则直线l1的斜率存在,设其方程为y=k1(x-2)+1,联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系求出A,B的横坐标的和与积,结合向量等式求得k1得答案.
解答 解:(1)设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1 (a>b>0),
由抛物线x2=-4$\sqrt{3}$y,得抛物线焦点F(0,-$\sqrt{3}$),
由题意得b=$\sqrt{3}$,$\frac{c}{a}$=$\frac{1}{2}$,解得a=2,c=1.
故椭圆C的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)∵过点P(2,1)的直线l与椭圆C在第一象限相切,∴直线l的斜率存在,
故可设直线l的方程为y=k(x-2)+1 (k≠0).
由 $\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=k(x-2)+1}\end{array}\right.$
得(3+4k2)x2-8k(2k-1 )x+16k2-16k-8=0.①
∵直线l与椭圆C相切,
∴△=[-8k(2k-1)]2-4(3+4k2)(16k2-16k-8)=0.
整理,得32(6k+3)=0,解得k=-$\frac{1}{2}$.
∴直线l的方程为y=-$\frac{1}{2}$(x-2)+1=-$\frac{1}{2}$x+2.
将k=-$\frac{1}{2}$代入①式,解得M点的横坐标为1,故切点M的坐标为;
(3)若存在直线l1满足条件,则直线l1的斜率存在,设其方程为y=k1(x-2)+1,
代入椭圆C的方程得:(3+4k)x2-8k1(2k1-1)x+16k-16k1 -8=0.
设A(x1,y1),B(x2,y2),
∵直线l1与椭圆C相交于不同的两点A,B,
∴△=[-8k1(2k1-1)]2-4(3+4k)(16k-16k1-8)=32(6k1+3)>0,得k1>-$\frac{1}{2}$.
x1+x2=$\frac{8{k}_{1}(2{k}_{1}-1)}{3+4{{k}_{1}}^{2}}$,x1x2=$\frac{16{{k}_{1}}^{2}-16{k}_{1}-8}{3+4{{k}_{1}}^{2}}$.
∵$\overrightarrow{PA}•\overrightarrow{PB}={\overrightarrow{PM}}^{2}$,即(x1-2)(x2-2)+(y1-1)(y2-1)=$\frac{5}{4}$,
∴(x1-2)(x2-2)(1+k)=$\frac{5}{4}$,即[x1x2-2(x1+x2)+4](1+k)=$\frac{5}{4}$,
∴[$\frac{8{k}_{1}(2{k}_{1}-1)}{3+4{{k}_{1}}^{2}}$-2$\frac{16{{k}_{1}}^{2}-16{k}_{1}-8}{3+4{{k}_{1}}^{2}}$+4](1+k)═$\frac{4+4{{k}_{1}}^{2}}{3+4{{k}_{1}}^{2}}$=$\frac{5}{4}$,
解得k1=±$\frac{1}{2}$.
∵A,B为不同的两点,∴k1=$\frac{1}{2}$.
于是存在直线l1满足条件,其方程为y=$\frac{1}{2}$x.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,体现了“设而不求”的解题思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $5+\sqrt{2}$ | C. | $4+\sqrt{2}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 重合 | B. | 形状相同,位置不同 | ||
| C. | 关于y轴对称 | D. | 形状不同,位置不同 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=4,EF=3,AD=AE=BE=2,G是BC的中点.
在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=4,EF=3,AD=AE=BE=2,G是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
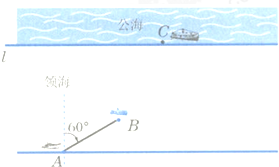 设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:
设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com