
分析 由$[\begin{array}{l}{a}&{k}\\{0}&{1}\end{array}]$$[\begin{array}{l}k\\-1\end{array}]$=λ$[\begin{array}{l}k\\-1\end{array}]$,即$\left\{\begin{array}{l}{ak-k=kλ}\\{-1=-λ}\end{array}\right.$,由k≠0,解得:$\left\{\begin{array}{l}{λ=1}\\{a=2}\end{array}\right.$,根据矩阵的运算性质可知:A$[\begin{array}{l}{1}\\{1}\end{array}]$=$[\begin{array}{l}{3}\\{1}\end{array}]$,$[\begin{array}{l}{2}&{k}\\{0}&{1}\end{array}]$$[\begin{array}{l}{1}\\{1}\end{array}]$=$[\begin{array}{l}{3}\\{1}\end{array}]$,即可求得k的值,求得a+k的值.
解答 解:设特征向量为$\overrightarrow{a}$=$[\begin{array}{l}k\\-1\end{array}]$,对应的特征值为λ,λ,
则$[\begin{array}{l}{a}&{k}\\{0}&{1}\end{array}]$$[\begin{array}{l}k\\-1\end{array}]$=λ$[\begin{array}{l}k\\-1\end{array}]$,即$\left\{\begin{array}{l}{ak-k=kλ}\\{-1=-λ}\end{array}\right.$,
由k≠0,解得:$\left\{\begin{array}{l}{λ=1}\\{a=2}\end{array}\right.$,
由A-1$[\begin{array}{l}{3}\\{1}\end{array}]$=$[\begin{array}{l}{1}\\{1}\end{array}]$,即A$[\begin{array}{l}{1}\\{1}\end{array}]$=$[\begin{array}{l}{3}\\{1}\end{array}]$,
$[\begin{array}{l}{2}&{k}\\{0}&{1}\end{array}]$$[\begin{array}{l}{1}\\{1}\end{array}]$=$[\begin{array}{l}{3}\\{1}\end{array}]$,即$\left\{\begin{array}{l}{2+k=3}\\{1=1}\end{array}\right.$,解得:k=1,
∴a+k=2+1=3,
故答案为:3.
点评 本题考查矩阵的运算,考查矩阵的特征值与特征向量的计算,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
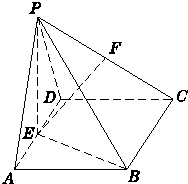 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面ABCD是边长为2的菱形,∠BAD=60°,E是AD的中点,F是PC的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面ABCD是边长为2的菱形,∠BAD=60°,E是AD的中点,F是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com