
分析 可过PAC∥PD,PE∥AB,分别交AB,AC于D,E,则得到四边形ADPE为平行四边形,从而可以得出$\overrightarrow{AD}=\frac{1}{6}\overrightarrow{AB},\overrightarrow{AE}=\frac{2}{5}\overrightarrow{AC}$,从而有DP∥AC,且$DP=\frac{2}{5}AC$,PE∥AB,且$PE=\frac{1}{6}AB$,从而可得到${S}_{△APB}=\frac{2}{5}{S}_{△ABC},{S}_{△APC}=\frac{1}{6}{S}_{△ABC}$,${S}_{△CPB}=\frac{13}{30}{S}_{△ABC}$,这样便可得出S△APB:S△CPB的值.
解答  解:如图,过P作AC∥PD,交AB于D,作PE∥AB,交AC于E,则:
解:如图,过P作AC∥PD,交AB于D,作PE∥AB,交AC于E,则:
四边形ADPE为平行四边形,$\overrightarrow{AP}=\overrightarrow{AD}+\overrightarrow{AE}$;
∴$\overrightarrow{AD}=\frac{1}{6}\overrightarrow{AB},\overrightarrow{AE}=\frac{2}{5}\overrightarrow{AC}$;
∴$DP=\frac{2}{5}AC,PE=\frac{1}{6}AB$;
∴${S}_{△APB}=\frac{2}{5}{S}_{△ABC},{S}_{△APC}=\frac{1}{6}{S}_{△ABC}$;
∴${S}_{△CPB}=\frac{13}{30}{S}_{△ABC}$;
∴S△APB:S△CPB=12:13.
故答案为:12:13.
点评 考查向量加法的平行四边形法则,平面向量基本定理,向量数乘的几何意义,以及三角形的面积公式.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年新疆库尔勒市高二上学期分班考试数学(理)试卷(解析版) 题型:解答题
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且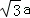 =2csinA
=2csinA
(1)确定角C的大小;
(2)若c=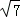 ,且△ABC的面积为
,且△ABC的面积为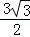 ,求a+b的值
,求a+b的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com