
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
分析 根据条件求出$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$,代入向量的夹角公式计算.
解答 解:∵(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)•(-2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$)=2$\sqrt{2}$-1,
∴-4${\overrightarrow{{e}_{1}}}^{2}$+3${\overrightarrow{{e}_{2}}}^{2}$+4$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=2$\sqrt{2}$-1.
∵${\overrightarrow{{e}_{1}}}^{2}$=${\overrightarrow{{e}_{2}}}^{2}$=1,
∴$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=$\frac{\sqrt{2}}{2}$.
∴cos<$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$>=$\frac{\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}}{|\overrightarrow{{e}_{1}}||\overrightarrow{{e}_{2}}|}$=$\frac{\sqrt{2}}{2}$.
∴<$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$>=$\frac{π}{4}$.
故选:A.
点评 本题考查了平面向量的数量积运算,属于基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 4 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(理)试卷(解析版) 题型:解答题
已知函数 (
(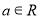 ).
).
(1)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)设 ,当
,当 时,若对任意
时,若对任意 ,存在
,存在 ,使
,使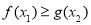 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com