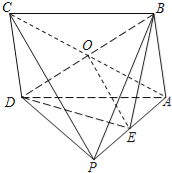
【题目】如图,在四棱锥
中,底面
为平行四边形, 
为侧棱
的中点.
（Ⅰ）求证: 
∥平面
（Ⅱ）若
,
,
求证:平面
平面
【答案】（1）（2）均见解析．
【解析】试题分析：（1）连结AC，交BD于O，连结OE，E为PA的中点，利用三角形中位线的性质，可知OE∥PC，利用线面平行的判定定理，即可得出结论；
（2）先证明PA⊥DE，再证明PA⊥OE，可得PA⊥平面BDE，从而可得平面BDE⊥平面PAB．
证明：（1）连结AC，交BD于O，连结OE．
因为ABCD是平行四边形，所以OA=OC．…（2分）
因为E为侧棱PA的中点，所以OE∥PC．…（4分）
因为PC平面BDE，OE平面BDE，所以PC∥平面BDE．…（6分）
（2）因为E为PA中点，PD=AD，所以PA⊥DE．…（8分）
因为PC⊥PA，OE∥PC，所以PA⊥OE．
因为OE平面BDE，DE平面BDE，OE∩DE=E，
所以PA⊥平面BDE．…（12分）
因为PA平面PAB，所以平面BDE⊥平面PAB．…（14分）
科目：高中数学 来源： 题型：
【题目】已知函数
， 
． 
在
上有最大值9，最小值4．
（1）求实数
的值；
（2）若不等式
在
上恒成立，求实数
的取值范围；
（3）若方程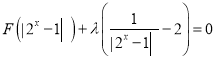
有三个不同的实数根，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点A是抛物线M：y2=2px（p＞0）与圆C：x2+（y﹣4）2=a2在第一象限的公共点，且点A到抛物线M焦点F的距离为a，若抛物线M上一动点到其准线与到点C的距离之和的最小值为2a，O为坐标原点，则直线OA被圆C所截得的弦长为（ ）
A.2
B.2 
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
）
（1）若
，用“五点法”在给定的坐标系中,画出函数
在[0,π]上的图象．
（2）若
偶函数，求
（3）在（2）的前提下，将函数
的图象向右平移
个单位后，再将得到的图象上各点的横坐标变为原来的4倍，纵坐标不变，得到函数
的图象，求
在
的单调递减区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“a=﹣1”是“直线ax+3y+2=0与直线x+（a﹣2）y+1=0平行”的（ ）
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目：高中数学 来源： 题型：
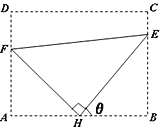
【题目】如图,某污水处理厂要在一个矩形污水处理池
的池底水平铺设污水净化管道（
， 
是直角顶点）来处理污水，管道越长，污水净化效果越好.设计要求管道的接口
是
的中点， 
分别落在线段
上.已知
米， 
米，记
.
（1）试将污水净化管道的总长度
(即
的周长)表示为
的函数，并求出定义域；
（2）问
当取何值时，污水净化效果最好？并求出此时管道的总长度.
（提示： 
.）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法中，正确的个数是（ ）
①函数f（x）=2x﹣x2的零点有2个；
②函数y=sin（2x+ 
）sin（ 
﹣2x）的最小正周期是π；
③命题“函数f（x）在x=x0处有极值，则f′（x0）=0”的否命题是真命题；
④ 
dx= 
．
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
