
分析 由二次函数f(x)同时满足下列两个个条件:(1)f(1+x)=f(1-x);(2)f(x)的最大值为15;可设f(x)=a(x-1)2+15(a<0).又f(x)=0的两根的平方和等于32.利用根与系数的关系即可得出a.
解答 解:由二次函数f(x)同时满足下列两个条件:
(1)f(1+x)=f(1-x);(2)f(x)的最大值为15;
说明其对称轴为x=1,抛物线开口向下.
可设f(x)=a(x-1)2+15(a<0).
化为f(x)=ax2-2ax+a+15,
设f(x)=0的两个实数根为x1,x2.
∴x1+x2=2,x1x2=$\frac{a+15}{a}$.(*)
∵f(x)=0的两根的平方和等于17,
∴${{x}_{1}}^{2}$+${{x}_{2}}^{2}$=17.
化为(x1+x2)2-2x1x2=17.
把(*)代入上式得22-2×$\frac{a+15}{a}$=17,解得a=-2.
∴f(x)=-2(x-1)2+15=-2x2+4x+13.
点评 本题综合考查了二次函数的对称性、最值及其零点等基础知识与基本方法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 先向左平移$\frac{π}{6}$个单位长度,再将所有点的横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变) | |
| B. | 先向左平移$\frac{π}{6}$个单位长度,再将所有点的横坐标缩短为原来的2倍(纵坐标不变) | |
| C. | 先将所有点的横坐标缩短为原来的2倍(纵坐标不变),再向左平移$\frac{π}{6}$个单位长度 | |
| D. | 先将所有点的横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变),再向左平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
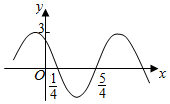
| A. | (kπ-$\frac{5}{4}$,kπ-$\frac{1}{4}$),k∈Z | B. | (2kπ-$\frac{5}{4}$,2kπ-$\frac{1}{4}$),k∈Z | ||
| C. | (2k-$\frac{5}{4}$,2k-$\frac{1}{4}$),k∈Z | D. | (k-$\frac{5}{4}$,k-$\frac{1}{4}$),k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<-$\frac{3}{8}$ | B. | x<-$\frac{1}{2}$ | C. | x≤-$\frac{1}{2}$ | D. | x≤-$\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
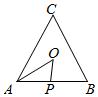 如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )
如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )| A. | 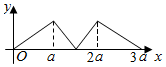 | B. | 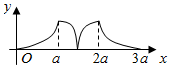 | ||
| C. | 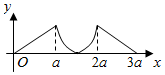 | D. | 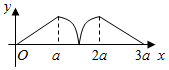 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com