
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 要判断“a<1”是“|x-2|+|x|>a恒成立”的条件,我们可先构造函数y=|x-2|+|x|并求出函数的值域,然后转化为一个恒成立的判断与性质问题,最后结合充要条件的定义,进行判断.
解答 解:函数y=|x-2|+|x|的值域为[2,+∞)
则当a<1时,|x-2|+|x|>a恒成立
反之若,|x-2|+|x|>a,则说明a小于函数y=|x-2|+|x|的最小值2恒成立,即a<2
故“a<1”是“|x-2|+|x|>a恒成立”的充分不必要条件
故选:A.
点评 判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | [-2,3) | C. | [-4,3) | D. | (-∞,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
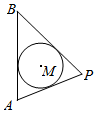 某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.
某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3\sqrt{3}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com