
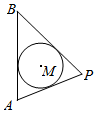
 某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.
某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.分析 (1)如图所示,设C,D,E分别为切点,设PD=x,OD=$\frac{1}{2}$,AC=BC=1.则OP=$\sqrt{(\frac{1}{2})^{2}+{x}^{2}}$.可得S△APB=$\frac{1}{2}PC•AB$=$\frac{1}{2}$•OD•(PA+PB+AB),解出即可得出.
(2)设AC=x,BC=y,PD=z,则x+y=2,S△PAB=$\frac{1}{2}$×$\frac{1}{2}$×(4+2z)=$\frac{1}{2}$(2+z),另一方面:S△PAB=$\sqrt{p[p-(x+y)][p-(x+z)][p-(y+z)]}$,其中p=$\frac{2+x+y+2z}{2}$=2+z.化简整理即可得出.
解答 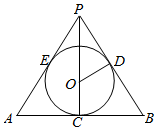 解:(1)如图所示,
解:(1)如图所示,
设C,D,E分别为切点,
设PD=x,OD=$\frac{1}{2}$,AC=BC=1.
则OP=$\sqrt{(\frac{1}{2})^{2}+{x}^{2}}$=$\sqrt{\frac{1}{4}+{x}^{2}}$.
∴S△APB=$\frac{1}{2}PC•AB$=$\frac{1}{2}$•OD•(PA+PB+AB),
∴$(\sqrt{\frac{1}{4}+{x}^{2}}+\frac{1}{2})$•2=$\frac{1}{2}×$(2x+2+2),
化为:3x2-2x=0,
解得x=$\frac{2}{3}$.
∴S△PAB=$\frac{1}{2}$×$\frac{1}{2}$×$(\frac{4}{3}+4)$=$\frac{4}{3}$.
(2)设AC=x,BC=y,PD=z,则x+y=2,
S△PAB=$\frac{1}{2}$×$\frac{1}{2}$×(4+2z)=$\frac{1}{2}$(2+z),
另一方面:S△PAB=$\sqrt{p[p-(x+y)][p-(x+z)][p-(y+z)]}$=$\sqrt{(2+z)z(2-x)(2-y)}$=$\sqrt{(2+z)zxy}$.其中p=$\frac{2+x+y+2z}{2}$=2+z.
∴$\frac{1}{2}$(2+z)=$\sqrt{(2+z)zxy}$,
化为$\frac{1}{4}$$(\frac{2}{z}+1)$=xy≤$(\frac{x+y}{2})^{2}$=1.
解得z$≥\frac{2}{3}$.
PA+PB=x+z+y+z=2+2z≥$\frac{10}{3}$.
点评 本题考查了直线与圆相切、三角形的内切圆的性质、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\root{3}{4}}}{2}$或1 | B. | $\frac{1}{2}$或1 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2\sqrt{14}}{7}$,$\frac{3\sqrt{2}}{2}$] | B. | [$\frac{2\sqrt{14}}{7}$,$\sqrt{2}$) | C. | [$\sqrt{2}$,$\frac{3\sqrt{2}}{2}$] | D. | [$\frac{3\sqrt{2}}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com