
分析 化简可得$\frac{{S}_{n+1}+{a}_{n+1}}{{S}_{n}+{a}_{n}}$=1,从而可得2an+1=an,从而求得an=$\frac{1}{{2}^{n}}$,4an+1=$\frac{1}{{2}^{n-2}}$+1,从而利用拆项求和法求得Tn=4-$\frac{1}{{2}^{n-2}}$+n,从而化不等式为k≥$\frac{2n-7}{12•{2}^{n-2}}$=$\frac{2n-7}{3•{2}^{n}}$,再令f(x)=$\frac{2x-7}{3•{2}^{x}}$,求导以确定函数的单调性,从而解得.
解答 解:∵数列{anSn+an2}也是公比为q的等比数列,
∴$\frac{{a}_{n+1}{S}_{n+1}+{a}_{n+1}^{2}}{{a}_{n}{S}_{n}+{a}_{n}^{2}}$=q•$\frac{{S}_{n+1}+{a}_{n+1}}{{S}_{n}+{a}_{n}}$=q,
∴$\frac{{S}_{n+1}+{a}_{n+1}}{{S}_{n}+{a}_{n}}$=1,
∴Sn+1+an+1=Sn+an,
∴2an+1=an,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{1}{2}$=q,
故an=$\frac{1}{{2}^{n}}$,4an+1=$\frac{1}{{2}^{n-2}}$+1,
故Tn=(2+1)+(1+1)+($\frac{1}{2}$+1)+($\frac{1}{4}$+1)+…+($\frac{1}{{2}^{n-2}}$+1)
=$\frac{2(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$+n
=4-$\frac{1}{{2}^{n-2}}$+n,
故$\frac{12k}{4+n-{T}_{n}}$≥2n-7可化为k≥$\frac{2n-7}{12•{2}^{n-2}}$=$\frac{2n-7}{3•{2}^{n}}$,
令f(x)=$\frac{2x-7}{3•{2}^{x}}$,
故f′(x)=$\frac{1}{3}$•$\frac{2•{2}^{x}-{2}^{x}ln2(2x-7)}{({2}^{x})^{2}}$
=$\frac{1}{3}$•$\frac{2+7ln2-(2ln2)x}{{2}^{x}}$,
故当x∈(0,$\frac{2+7ln2}{2ln2}$)时,f′(x)>0,
当x∈($\frac{2+7ln2}{2ln2}$,+∞)时,f′(x)<0,
故f(x)在(0,$\frac{2+7ln2}{2ln2}$)上单调递增,在($\frac{2+7ln2}{2ln2}$,+∞)上单调递减;
而4<$\frac{2+7ln2}{2ln2}$<5,
$\frac{8-7}{3×16}$=$\frac{1}{48}$,$\frac{10-7}{3×32}$=$\frac{1}{32}$,
故只需使k≥$\frac{1}{32}$.
故答案为:k≥$\frac{1}{32}$.
点评 本题考查了导数的综合应用及数列的通项公式及前n项和公式的应用,同时考查了拆项求和法的应用及构造法的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
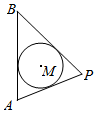 某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.
某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com