
 如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,
如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,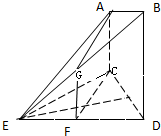
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
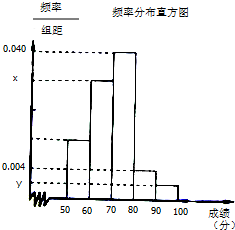 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题:| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | 0.08 | |
| 第5组 | [90,100) | 2 | b |
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若DE=4
将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若DE=4| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 树干周长(单位:cm) | [30,40) | [40,50) | [50,60) | [60,70) |
| 杉树 | 6 | 19 | 21 | x |
| 槐树 | 4 | 20 | y | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
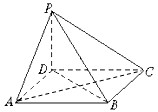 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.查看答案和解析>>
科目:高中数学 来源: 题型:
| ax2 |
| 2 |
| 3 |
| 2a |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.
如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com