
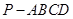 中,
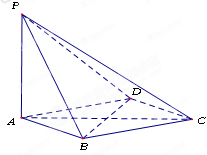
中,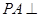 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,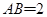 ,
,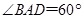 .
.
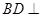 平面PAC;
平面PAC;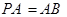 ,求
,求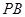 与
与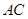 所成角的余弦值;
所成角的余弦值;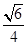 ;(3)
;(3)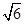 .
.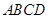 是菱形,所以
是菱形,所以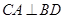 ,另外一条直线当然考虑
,另外一条直线当然考虑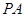 (或者
(或者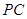 ),本题中应该是
),本题中应该是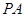 ;(2)求异面直线所成的角,一般可通过平移变成相交直线所成的角,考虑到第(3)小题问题,且题中有垂直的直线,故考虑建立空间直角坐标系(以
;(2)求异面直线所成的角,一般可通过平移变成相交直线所成的角,考虑到第(3)小题问题,且题中有垂直的直线,故考虑建立空间直角坐标系(以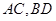 的交点
的交点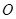 为坐标原点,
为坐标原点,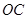 为
为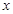 轴,
轴,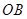 为
为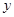 轴,过
轴,过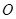 与
与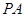 平行的直线为
平行的直线为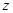 轴),则
轴),则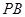 与
与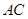 所成角就是
所成角就是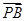 与
与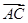 的夹角((锐角(或其补角)或直角),平面
的夹角((锐角(或其补角)或直角),平面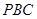 与平面
与平面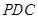 垂直就是它们的法向量垂直,即它们的法向量的数量积为0.
垂直就是它们的法向量垂直,即它们的法向量的数量积为0.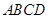 是菱形,所以
是菱形,所以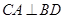 ,又因为
,又因为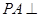 平面
平面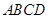 ,所以
,所以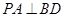 ,而
,而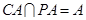 ,所以
,所以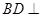 平面
平面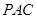 .
.
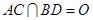 ,因为
,因为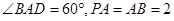 ,
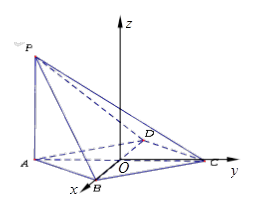
,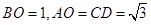 ,如图,以
,如图,以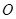 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系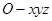 ,则
,则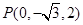 ,
,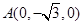 ,
,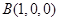 ,
,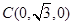 ,
,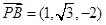 ,
,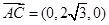 ,设
,设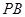 与
与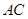 所成的角为
所成的角为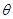 ,则
,则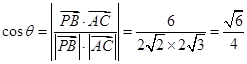 .
.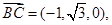 设
设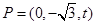
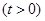 .则
.则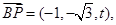 设平面
设平面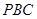 的法
的法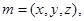 则
则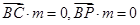 ,所以
,所以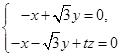 令
令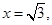 则
则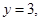
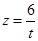 ,
,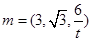 同理,平面
同理,平面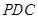 的法向量
的法向量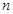
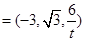 ,因为平面
,因为平面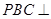
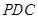 ,所以
,所以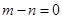 ,即
,即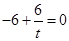 解得
解得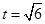 ,所以
,所以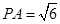 .
.

 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源:不详 题型:解答题
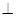 底面ABCD,SA=AD,点M是SD的中点,AN
底面ABCD,SA=AD,点M是SD的中点,AN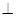 SC且交SC于点N.
SC且交SC于点N.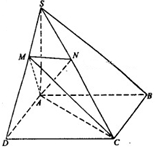
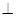 平面AMN.
平面AMN.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com