
分析 (Ⅰ)根据导数的几何意义即可求出.
(Ⅱ)若对任意的x∈[0,+∞),h(x)≤$\frac{1}{2}$x恒成立,则f(x)-g(x)≤0恒成立,g(x)=ax2+ln(x+1)-x,(x≥0),只需g(x)max≤0,分类讨论后,综合讨论结果可得实数a的取值范围.
解答 解:(Ⅰ)f(0)=0,所以切点为(0,0),
∵f′(x)=2ax-$\frac{1}{2}$+$\frac{2}{x+1}$,
∴f′(0)=-$\frac{1}{2}$+2=$\frac{3}{2}$,
∴所求切线方程为y=$\frac{3}{2}$x,
(Ⅱ)由题设,当x∈[0,+∞)时,不等式ax2+ln(x+1)-x≤0恒成立,
设g(x)=ax2+ln(x+1)-x,(x≥0),只需g(x)max≤0即可,
由g′(x)=2ax+$\frac{1}{a+1}$-1=$\frac{x(2ax+2a-1)}{x+1}$,
(1)当a=0时,g′(x)=-$\frac{x}{x+1}$,
当x>0时,g′(x)<0,函数g(x)在[0,+∞)上单调递减,
故g(x)max=g(0)=0,满足条件,
(2)当a>0时,令g′(x)=$\frac{[2ax+(2a-1)]}{x+1}$=0,解得x=$\frac{1}{2a}$-1,
①若$\frac{1}{2a}$-1≤0,即a≥$\frac{1}{2}$,在区间(0,+∞)上,g′(x)>0,
则函数g(x)在[0,+∞)上单调递增,g(x)≥0,当且仅当x=0时等号成立,此时不满足条件,
②若$\frac{1}{2a}$-1>0,即0<a<$\frac{1}{2}$时,函数g(x)在(0,$\frac{1}{2a}$-1)上单调递减,在区间($\frac{1}{2a}$-1,+∞)上单调递增,
g($\frac{1}{a}$)=lg(1+$\frac{1}{a}$)>0,此时不满足条件,
(3)当a<0时,由g′(x)=$\frac{[2ax+(2a-1)]}{x+1}$,
∴2ax+(2a-1)<1,
∴g′(x)<0,函数g(x)在[0,+∞)上单调递减,
故g(x)max=g(0)=0,满足条件,
综上所述,实数a的取值范围为(-∞,0]
点评 本题考查的知识点是利用导数求闭区间上的函数最值,利用导数研究函数的单调性,熟练掌握导数符号与原函数单调性的关系,是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=2x2-x+1在(0,+∞)上是增函数 | |
| B. | 幂函数在(0,+∞)上都是增函数 | |
| C. | 函数y=log2(x+$\sqrt{{x}^{2}+1}$)既不是奇函数,也不是偶函数 | |
| D. | 已知f(x)是定义在R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x0)<x0 | B. | f(x0)=x0 | C. | f(x0)>x0 | D. | f(x0)=-x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
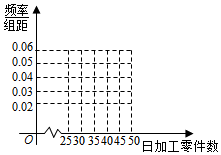 随机观测生产某种们零件的某工厂20名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,48,37,25,45,43,31,49,34,33,43,38,32,46,39,36.根据上述数据得到样本的频率分布表如下:
随机观测生产某种们零件的某工厂20名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,48,37,25,45,43,31,49,34,33,43,38,32,46,39,36.根据上述数据得到样本的频率分布表如下:| 分组 | 频数 | 频率 |
| [25,30] | 2 | 0.10 |
| (30,35] | 4 | 0.20 |
| (35,40] | 5 | 0.25 |
| (40,45] | m | fm |
| (45,50] | n | fn |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com