Question

17．对于曲线C所在平面内的点O，若存在以O为顶点的角θ，使得θ≥∠AOB对于曲线C上的任意两个不同点A、B恒成立，则称θ为曲线C相对于O的“界角”，并称最小的“界角”为曲线C相对于O的“确界角”，已知曲线M：y=$\left\{\begin{array}{l}{\sqrt{1+9{x}^{2}}，x≤0}\\{1+x{e}^{x-1}，x＞0}\end{array}\right.$，（其中e为自然对数的底数），O为坐标原点，则曲线M相对于O的“确界角”为（　　）

• A． $\frac{π}{3}$
• B． $\frac{π}{4}$
• C． $\frac{2π}{3}$
• D． $\frac{3π}{4}$

Answer 1

分析 画出函数f（x）的图象，过点O作出两条直线与曲线无限接近，当x≤0时，曲线y=$\sqrt{1+9{x}^{2}}$与直线y=k₁x无限接近，考虑渐近线，求出k₁=-3；当x＞0时，设出切点，求出切线的斜率，列出方程，求出切点（1，2），即得k₂=2，再由两直线的夹角公式即可得到所求的“确界角”．

解答 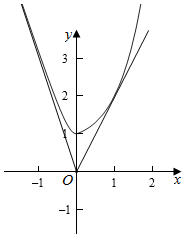解：画出函数f（x）的图象，过点O作出两条直线与曲线无限接近，设它们的方程分别为y=k₁x，y=k₂x，
当x≤0时，曲线y=$\sqrt{1+9{x}^{2}}$与直线y=k₁x无限接近，即为双曲线的渐近线，故k₁=-3；
当x＞0时，y′=e^x-1+xe^x-1，设切点为（m，n），则n=k₂m，
n=me^m-1+1，k₂=e^m-1+me^m-1，即有m²e^m-1=1，
由x²e^x-1（x＞0）为增函数，且x=1成立，故m=1，k₂=2，
由两直线的夹角公式得，tanθ=|$\frac{2-（-3）}{1+2×（-3）}$|=1，
故曲线C相对于点O的“确界角”为$\frac{π}{4}$．
故选：B．

点评 本题考查新定义“确界角”及应用，考查导数的应用：求切线，双曲线的性质：渐近线，属于中档题．