
| A. | y=2|x| | B. | $y=\frac{1}{x^2}$ | C. | y=|lgx| | D. | y=cosx |
分析 根据偶函数的定义,偶函数定义域的特点,二次函数的单调性,指数函数的单调性,以及减函数的定义,余弦函数的单调性便可判断每个选项的正误,从而找出正确选项.
解答 解:A.y=2|x|,显然该函数为偶函数;x∈(0,+∞)时,y=2x为增函数,∴该选项正确;
B.$y=\frac{1}{{x}^{2}}$,x∈(0,+∞)时,y=x2为增函数;∴x增大时,$\frac{1}{{x}^{2}}$减小,即y减小;
∴该函数在(0,+∞)上为减函数,∴该选项错误;
C.y=|lgx|的定义域为(0,+∞),不关于原点对称,不是偶函数,∴该选项错误;
D.y=cosx在(0,+∞)上没有单调性,∴该选项错误.
故选A.
点评 考查偶函数的定义,偶函数定义域的对称性,二次函数、指数函数及余弦函数的单调性,以及减函数的定义.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
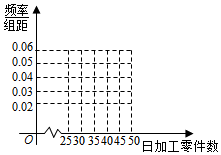 随机观测生产某种们零件的某工厂20名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,48,37,25,45,43,31,49,34,33,43,38,32,46,39,36.根据上述数据得到样本的频率分布表如下:
随机观测生产某种们零件的某工厂20名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,48,37,25,45,43,31,49,34,33,43,38,32,46,39,36.根据上述数据得到样本的频率分布表如下:| 分组 | 频数 | 频率 |
| [25,30] | 2 | 0.10 |
| (30,35] | 4 | 0.20 |
| (35,40] | 5 | 0.25 |
| (40,45] | m | fm |
| (45,50] | n | fn |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com