
分析 计算定积分,求出f(x)的解析式,令$\left\{\begin{array}{l}{a-3<0}\\{f(1)>f(2)}\end{array}\right.$解不等式组得出a的范围.
解答 解:由定积分的几何意义可知:${∫}_{-2}^{2}$$\sqrt{4-{t}^{2}}$dt=$\frac{1}{2}$π×22=2π,
∴f(x)=$\left\{\begin{array}{l}{(a-3)x,x≥2}\\{(\frac{1}{3})^{x}-1,x<2}\end{array}\right.$,
∴a1=f(1)=-$\frac{2}{3}$,n≥2时,an=f(n)=(a-3)n,
∵数列{an}是单调递减数列,
∴$\left\{\begin{array}{l}{-\frac{2}{3}>2(a-3)}\\{a-3<0}\end{array}\right.$,解得a<$\frac{8}{3}$.
故答案为:(-∞,$\frac{8}{3}$).
点评 本题考查了定积分的计算,数列单调性的判断,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2cosθ,2sinθ) | B. | (-2cosθ,2sinθ) | C. | (-2cosθ,-2sinθ) | D. | (2cosθ,-2sinθ) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{3\sqrt{3}}{5}$ | C. | $\frac{\sqrt{3}}{19}$ | D. | $\frac{\sqrt{3}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
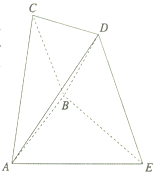 在如图所示的空间几何体中,边长为2的正三角形ABC所在平面与正三角形ABE所在平面互相垂直,DE在平面ABE内的射影为∠AEB的平分线且DE与平面AEB所成的角为60°,DE=2.
在如图所示的空间几何体中,边长为2的正三角形ABC所在平面与正三角形ABE所在平面互相垂直,DE在平面ABE内的射影为∠AEB的平分线且DE与平面AEB所成的角为60°,DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
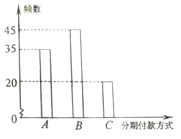 某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.
某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com