
| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{3\sqrt{3}}{5}$ | C. | $\frac{\sqrt{3}}{19}$ | D. | $\frac{\sqrt{3}}{7}$ |
分析 由tan(α+80°)=4sin420°=4sin60°=2$\sqrt{3}$,利用构造的思想,tan(α+20°)=tan[(α+80°)-60°]利用正切的和与差的公式打开可得答案.
解答 解:由tan(α+80°)=4sin420°=4sin60°=2$\sqrt{3}$,
那么:tan(α+20°)=tan[(α+80°)-60°]=$\frac{tan(α+80°)-tan60°}{1+tan(α+80°)tan60°}$=$\frac{2\sqrt{3}-\sqrt{3}}{1+2\sqrt{3}×\sqrt{3}}=\frac{\sqrt{3}}{7}$.
故选D.
点评 本题主要考查正切的和与差公式和诱导公式的化简,利用了构造的思想.属于基础题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{12}$个长度单位 | B. | 向右平移$\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{5π}{12}$个长度单位 | D. | 向右平移$\frac{5π}{12}$个长度单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{3\sqrt{3}}{5}$ | C. | $\frac{\sqrt{3}}{7}$ | D. | $\frac{\sqrt{3}}{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
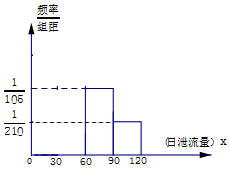 某地政府在该地一水库上建造一座水电站,用泄流水量发电,如图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120],历年中日泄流量在区间[30,60)的年平均天数为156天,一年按364天计.
某地政府在该地一水库上建造一座水电站,用泄流水量发电,如图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120],历年中日泄流量在区间[30,60)的年平均天数为156天,一年按364天计.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com