
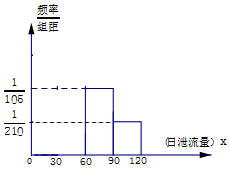
 某地政府在该地一水库上建造一座水电站,用泄流水量发电,如图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120],历年中日泄流量在区间[30,60)的年平均天数为156天,一年按364天计.
某地政府在该地一水库上建造一座水电站,用泄流水量发电,如图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120],历年中日泄流量在区间[30,60)的年平均天数为156天,一年按364天计.分析 (Ⅰ)设在区间[0,30)上,$\frac{频率}{组距}$=a,由频率分布直方图的性质求出a=$\frac{1}{210}$,由此能补充完整频率分布直方图.
(Ⅱ)记水电站日利润为Y元.不能运行发电机的概率为$\frac{1}{7}$,恰好运行一台发电机的概率为$\frac{3}{7}$,恰好运行二台发电机的概率为$\frac{2}{7}$,恰好运行三台发电机的概率为$\frac{1}{7}$,分别求出安装1台发电机、安装2台发电机、安装3台发电机的数学期望,由此得到要使水电站日利润的期望值最大,该水电站应安装3台发电机.
解答 解:(Ⅰ)在区间[30,60)的频率为$\frac{156}{364}=\frac{3}{7}$,(1分)
$\frac{频率}{组距}$=$\frac{3}{7×30}$=$\frac{1}{70}$,(2分)
设在区间[0,30)上,$\frac{频率}{组距}$=a,
则(a+$\frac{1}{70}+\frac{1}{105}+\frac{1}{210}$)×30=1,
解得a=$\frac{1}{210}$,(3分)
补充频率分布直方图如右图所示.(6分)
(Ⅱ)记水电站日利润为Y元.由(Ⅰ)知:不能运行发电机的概率为$\frac{1}{7}$,
恰好运行一台发电机的概率为$\frac{3}{7}$,恰好运行二台发电机的概率为$\frac{2}{7}$,
恰好运行三台发电机的概率为$\frac{1}{7}$,
①若安装1台发电机,则Y的值为-500,4000,其分布列为:
| Y | -500 | 4000 |
| P | $\frac{1}{7}$ | $\frac{6}{7}$ |
| Y | -1000 | 3500 | 8000 |
| P | $\frac{1}{7}$ | $\frac{3}{7}$ | $\frac{3}{7}$ |
| Y | -1500 | 3000 | 7500 | 12000 |
| P | $\frac{1}{7}$ | $\frac{3}{7}$ | $\frac{2}{7}$ | $\frac{1}{7}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意频率分布直方图、相互独立事件概率乘法公式的合理运用.


科目:高中数学 来源: 题型:填空题
 在直角梯形ABCD中,AB∥DC,AD⊥AB,AD=AB=2DC=2,点E、F分别在线段DC、AB上,设$\overrightarrow{DE}$=λ$\overrightarrow{DC}$,$\overrightarrow{AF}$=λ$\overrightarrow{AB}$,则$\overrightarrow{AE}$•$\overrightarrow{CF}$的最小值为-$\frac{33}{8}$.
在直角梯形ABCD中,AB∥DC,AD⊥AB,AD=AB=2DC=2,点E、F分别在线段DC、AB上,设$\overrightarrow{DE}$=λ$\overrightarrow{DC}$,$\overrightarrow{AF}$=λ$\overrightarrow{AB}$,则$\overrightarrow{AE}$•$\overrightarrow{CF}$的最小值为-$\frac{33}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{3\sqrt{3}}{5}$ | C. | $\frac{\sqrt{3}}{19}$ | D. | $\frac{\sqrt{3}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
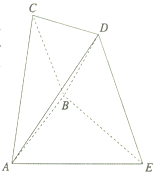 在如图所示的空间几何体中,边长为2的正三角形ABC所在平面与正三角形ABE所在平面互相垂直,DE在平面ABE内的射影为∠AEB的平分线且DE与平面AEB所成的角为60°,DE=2.
在如图所示的空间几何体中,边长为2的正三角形ABC所在平面与正三角形ABE所在平面互相垂直,DE在平面ABE内的射影为∠AEB的平分线且DE与平面AEB所成的角为60°,DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
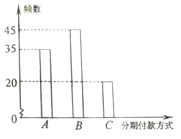 某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.
某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 12 | C. | 24 | D. | 36 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com