
【题目】已知函数f(x)=sin(![]() -x)sin x-
-x)sin x-![]() cos2x.
cos2x.
(1)求f(x)的最小正周期和最大值;
(2)讨论f(x)在(![]() )上的单调性.
)上的单调性.
【答案】(1)最小正周期π,最大值![]() ; (2)见解析
; (2)见解析
【解析】试题分析:(1)由条件利用诱导公式、二倍角的正弦公式、二倍角的余弦公式以及辅助角公式化简函数的解析式,再利用正弦函数的周期公式可得函数的周期,根据三角函数的有界性求得![]() 的最大值;(2)根据
的最大值;(2)根据![]() 可得
可得![]() ,利用正弦函数的单调性,分类讨论求由
,利用正弦函数的单调性,分类讨论求由![]() ,
, ![]() 可求得
可求得![]() 在
在![]() 上的单调区间.
上的单调区间.
试题解析:(1)f(x)=sin(![]() -x)sin x-
-x)sin x-![]() cos2x=cos xsin x-
cos2x=cos xsin x-![]() (1+cos 2x)
(1+cos 2x)
=![]() sin 2x-
sin 2x-![]() cos 2x-
cos 2x-![]() =sin(2x-
=sin(2x-![]() )-
)-![]() ,
,
因此f(x)的最小正周期为π,最大值为![]() .
.
(2)当x∈![]() ,
,![]() 时,0≤2x-
时,0≤2x-![]() ≤π,从而
≤π,从而
当0≤2x-![]() ≤
≤![]() ,即
,即![]() ≤x≤
≤x≤![]() 时,f(x)单调递增;
时,f(x)单调递增;
当![]() ≤2x-
≤2x-![]() ≤π,即
≤π,即![]() ≤x≤
≤x≤![]() 时,f(x)单调递减.
时,f(x)单调递减.
综上可知,f(x)在![]() ,
,![]() 上单调递增;在
上单调递增;在![]() ,
,![]() 上单调递减.
上单调递减.


科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:在定义域
满足:在定义域![]() 内存在实数
内存在实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 为“
为“![]() 的饱和函数”.给出下列四个函数:①
的饱和函数”.给出下列四个函数:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() .其中是“
.其中是“![]() 的饱和函数”的所有函数的序号是______________.
的饱和函数”的所有函数的序号是______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导数f′(x),x∈R,有f(﹣x)+f(x)=x2 , 在(0,+∞)上f′(x)<x,若f(6﹣m)﹣f(m)﹣18+6m≥0,则实数m的取值范围为( )
A.[﹣3,3]
B.[3,+∞)
C.[2,+∞)
D.(﹣∞,﹣2]∪[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税》规定,公民月工资、薪金所得不超过3500元的部分不纳税,超过3500元的部分为全月纳税所得额,此项税款按下表分段累计计算:

已知张先生的月工资、薪金所得为10000元,问他当月应缴纳多少个人所得税?
设王先生的月工资、薪金所得为![]() 元,当月应缴纳个人所得税为
元,当月应缴纳个人所得税为![]() 元,写出
元,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)已知王先生一月份应缴纳个人所得税为303元,那么他当月的个工资、薪金所得为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的圆心为
的圆心为 ![]() 的圆心为N,一动圆与圆M内切,与圆N外切.
的圆心为N,一动圆与圆M内切,与圆N外切.
(1)求动圆圆心P的轨方迹方程;
(2)设A,B分别为曲线P与x轴的左右两个交点,过点 ![]() 的直线
的直线 ![]() 与曲线P交于C,D两点,若
与曲线P交于C,D两点,若 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为 ![]() 的等比数列{an}不是递减数列,其前n项和为Sn (n∈N*),且S3+a3 , S5+a5 , S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn (n∈N*),且S3+a3 , S5+a5 , S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)若实数a使得a>Sn+ ![]() 对任意n∈N*恒成立,求a的取值范围.
对任意n∈N*恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 ![]() 以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A,B两点.
以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A,B两点.
(1)写出直线l的极坐标方程与曲线C的普通方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA||MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.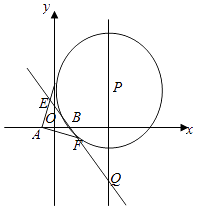
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com