
【题目】命题p:关于x的不等式x2+2ax+4>0对于一切x∈R恒成立,命题q:x∈11,2],x2-a≥0,若p∨q为真,p∧q为假,求实数a的取值范围.
【答案】{a|1<a<2或a≤-2}
【解析】
试题分析:根据二次函数的图象和性质我们可以求出命题p:关于x的不等式x2+2ax+4>0对于一切x∈R恒成立时,及命题q:x∈[1,2],x2-a≥0时,a的取值范围,根据p∨q为真,p∧q为假,结合复合命题的真值表,可得p、q一真一假,分类讨论后可得实数a的取值范围
试题解析:设g(x)=x2+2ax+4,由于关于x的不等式x2+2ax+4>0对于一切x∈R恒成立,所以g(x)函数的图象开口向上且与x轴没有交点,故Δ=4a2-16<0,所以-2<a<2.
若q为真命题,a≤x2恒成立,即a≤1.由于p或q为真,p且q为假,可知p、q一真一假.
①若p真q假,则![]() 所以1<a<2;
所以1<a<2;
②若p假q真,则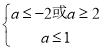 所以a≤-2;
所以a≤-2;
综上可知,所求实数a的取值范围是{a|1<a<2或a≤-2}


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】设![]() 实数
实数![]() 满足不等式
满足不等式![]() 函数
函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在互联网时代,网校培训已经成为青年学习的一种趋势,假设某网校的套题每日的销售量![]() (单位:千套)与销售价格
(单位:千套)与销售价格![]() (单位:元/套)满足的关系式
(单位:元/套)满足的关系式![]() (
(![]() ,
,![]() 为常数),其中
为常数),其中![]() 与
与![]() 成反比,
成反比,![]() 与
与![]() 的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
(1) 求![]() 的表达式;
的表达式;
(2) 假设网校的员工工资,办公等所有开销折合为每套题3元(只考虑销售出的套数),试确定销售价格![]() 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆x2+y2-6x-8y+21=0和直线kx-y-4k+3=0.
(1)若直线和圆总有两个不同的公共点,求k的取值集合
(2)求当k取何值时,直线被圆截得的弦最短,并求这最短弦的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=2![]() ,记动点P的轨迹为W.
,记动点P的轨迹为W.
⑴求W的方程;
⑵若A、B是W上的不同两点,O是坐标原点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次“知识竞赛”活动中,有![]() 四道题,其中
四道题,其中![]() 为难度相同的容易题,
为难度相同的容易题, ![]() 为中档题,
为中档题, ![]() 为较难题,现甲、乙两位同学均需从四道题目中随机抽取一题作答.
为较难题,现甲、乙两位同学均需从四道题目中随机抽取一题作答.
(1)求甲、乙两位同学所选的题目难度相同的概率;
(2)求甲所选题目的难度大于乙所选题目的难度的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列说法中正确的有( )
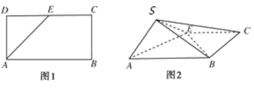
①存在点E使得直线SA⊥平面SBC;
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行;
④存在点E使得SE⊥BA.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业共有20条生产线,由于受生产能力和技术水平等因素的影响,会产生一定量的次品.根据经验知道,每台机器产生的次品数![]() 万件与每台机器的日产量
万件与每台机器的日产量![]() 万件
万件![]() 之间满足关系:
之间满足关系: ![]() .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
(Ⅰ)试将该企业每天生产这种产品所获得的利润![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)当每台机器的日产量为多少时,该企业的利润最大,最大为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com