考点:数列与不等式的综合
专题:计算题,证明题,导数的综合应用,不等式的解法及应用
分析:(1)求出导数,由极值的定义,得f′(
)=0,得a
n+1=
a
n+2
-n,由b
n=2
n-1•a
n,则b
n+1-b
n=1,由等差数列的通项公式即可得到;
(2)运用错位相减法求数列的和,注意解题步骤,运用等比数列求和公式即可得到;
(3)运用二项式定理,展开2
n=(1+1)
n,即可得证.
解答:
(1)解:f′(x)=a
nx+2
-n-a
n+1,
由题意得f′(
)=0,得a
n+1=
a
n+2
-n,
由a
n+1=
a
n+2
-n,得2
na
n+1-2
n-1•a
n=1,
由b
n=2
n-1•a
n,则b
n+1-b
n=1,
则数列{b
n}的通项公式b
n=b
1+(n-1)×1=1+n-1=n;
(2)解:由(1)得,a
n=n•2
1-n,
则S
n=1•2
1-1+2×2
1-2+3×2
1-3+…+(n-1)×2
1-(n-1)+n•2
1-n,
2S
n=1×2+2×2
1-1+3×2
1-2+…+n•2
2-n,
两式相减得,S
n=1×2+1×2
1-1+1×2
1-2+1×2
1-3+…+1×2
1-(n-1)-n•2
1-n=
-n•2
1-n=4-
;
(3)证明:由S
n=4-
=4-
=4-
n>3时,S
n>4-
=4-
=4-
=
.
点评:本题考查导数的运用:求极值,考查数列的通项公式的求法,注意构造数列,运用等差数列的通项公式和等比数列求和公式,考查错位相减求和,以及二项式定理用于证明不等式的方法,属于中档题和易错题.



 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案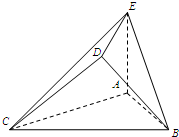 如图,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
如图,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.