
 已知在四棱锥C-ABDE中,DB⊥平面ABC,AE∥DB,△ABC是边长为2的等边三角形,AE=1,M为AB的中点.
已知在四棱锥C-ABDE中,DB⊥平面ABC,AE∥DB,△ABC是边长为2的等边三角形,AE=1,M为AB的中点.分析 (1)推导出CM⊥AB,DB⊥CM,从而CM⊥平面ABDE,由此能证明CM⊥EM.
(2)以点M为坐标原点,MC,MB所在直线分别为x,y轴,过M且与直线BD平行的直线为z轴,建立空间直角坐标系,利用向量法能求出二面角B-CD-E的大小.
解答 证明:(1)∵△ABC是等边三角形,M为AB的中点,∴CM⊥AB.
又∵DB⊥平面ABC,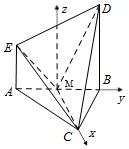
∴DB⊥CM,∴CM⊥平面ABDE,
∵EM?平面ABDE,∴CM⊥EM.(4分)
解:(2)如图,以点M为坐标原点,MC,MB所在直线分别为x,y轴,
过M且与直线BD平行的直线为z轴,建立空间直角坐标系.
∵DB⊥平面ABC,∴∠DMB为直线DM与平面ABC所成的角.(6分)
由题意得tan$∠DMB=\frac{BD}{MB}=2$,即BD=2,故B(0,1,0),C($\sqrt{3},0,0$),D(0,1,2),E(0,-1,1),
∴$\overrightarrow{BC}$=($\sqrt{3},-1,0$),$\overrightarrow{BD}$=(0,0,2),$\overrightarrow{CE}$=(-$\sqrt{3},-1,1$),$\overrightarrow{CD}$=(-$\sqrt{3},1,2$),
设平面BCD与平面CDE的法向量分别为$\overrightarrow{m}$=(x,y,z),$\overrightarrow{n}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BC}=\sqrt{3}x-y=0}\\{\overrightarrow{m}•\overrightarrow{BD}=2z=0}\end{array}\right.$,令x=1,得$\overrightarrow{m}$=(1,$\sqrt{3}$,0).
同理求得$\overrightarrow{n}$=(1,-$\frac{\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$),(10分)
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=0,∴二面角B-CD-E的大小为90°.(12分)
点评 本题考查线线垂直的证明,考查二面角的大小的求法,考查空间中线线、线面、面面间的位置关系,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 7 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | 4π | C. | 2π | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-12,1] | B. | [-12,0] | C. | [-2,4] | D. | [1,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
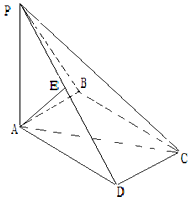 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=90°,四边形ABCD是平行四边形,且PA=AD=2,AB=1,E是线段PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=90°,四边形ABCD是平行四边形,且PA=AD=2,AB=1,E是线段PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{72.8}{81}$ | B. | $\frac{182}{81}$ | C. | $\frac{364}{81}$ | D. | $\frac{91}{81}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com