
分析 (Ⅰ)利用分段函数的性质求出分段函数的表达式,即可求出f(x)的单调区间;
(Ⅱ)讨论a的取值范围结合函数f(x)有两个零点,构造函数,结合一元二次函数的性质进行求解即可.
解答 解:(Ⅰ)$f(x)={x^2}-x|{x-1}|-3=\left\{\begin{array}{l}2{x^2}-x-3,x≤1\\ x-3,x>1.\end{array}\right.$
根据函数的图象可得,f(x)在$({-∞,\frac{1}{4}})$上单调递减,在$({\frac{1}{4},+∞})$上单调递增.-----------------------(6分)
(Ⅱ)$f(x)={x^2}-x|{x-a}|-3a=\left\{\begin{array}{l}2{x^2}-ax-3a,x≤a\\ ax-3a,x>a.\end{array}\right.$
①当0<a<3时,令f(x)=0,
可得${x_1}=3,{x_2}=\frac{{a-\sqrt{{a^2}+24a}}}{4}$,${x_3}=\frac{{a+\sqrt{{a^2}+24a}}}{4}$(因为f(a)=a2-3a<0,所以x3>a舍去)--------------------(8分)
所以$|{\frac{1}{x_1}-\frac{1}{x_2}}|=\frac{1}{3}+\frac{4}{{\sqrt{{a^2}+24a}-a}}=\frac{1}{3}+\frac{{\sqrt{{a^2}+24a}+a}}{6a}=\frac{1}{2}+\frac{1}{6}\sqrt{1+\frac{24}{a}}$,
在0<a<3上是减函数,所以$|{\frac{1}{x_1}-\frac{1}{x_2}}|∈({1,+∞})$.-----------------------------(11分)
②当a≥3时,令f(x)=0,则可得x1,x2是方程2x2-ax-3a=0的两个根,
所以$|{\frac{1}{x_1}-\frac{1}{x_2}}|=\frac{{|{{x_1}-{x_2}}|}}{{|{{x_1}{x_2}}|}}=\frac{{\sqrt{{a^2}+24a}}}{3a}=\frac{1}{3}\sqrt{1+\frac{24}{a}}∈({\frac{1}{3},1}]$,------------------(14分)
综合①②得,$|{\frac{1}{x_1}-\frac{1}{x_2}}|∈({\frac{1}{3},+∞})$.-------------------------------------(15分)
点评 本题主要考查函数单调性和函数零点的应用,根据分段函数的性质是解决本题的关键.综合性较强,难度较大.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 赞成禁放 | 不赞成禁放 | 合计 | |
| 老年人 | 60 | 140 | 200 |
| 中青年人 | 80 | 120 | 200 |
| 合计 | 140 | 260 | 400 |
| P(k2>k0) | 0.050 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -16 | C. | 55 | D. | 101 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
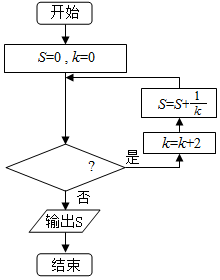
| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com