
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的一个动点,当直线
上的一个动点,当直线![]() 的斜率等于
的斜率等于![]() 时,
时,![]() 轴.
轴.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,试判断以
,试判断以![]() 为直径的圆是否过
为直径的圆是否过![]() 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.
科目:高中数学 来源: 题型:
【题目】改革开放以来,我国经济持续高速增长![]() 如图给出了我国2003年至2012年第二产业增加值与第一产业增加值的差值
如图给出了我国2003年至2012年第二产业增加值与第一产业增加值的差值![]() 以下简称为:产业差值
以下简称为:产业差值![]() 的折线图,记产业差值为
的折线图,记产业差值为![]() 单位:万亿元
单位:万亿元![]() .
.
![]() 求出y关于年份代码t的线性回归方程;
求出y关于年份代码t的线性回归方程;
![]() 利用
利用![]() 中的回归方程,分析2003年至2012年我国产业差值的变化情况,并预测我国产业差值在哪一年约为34万亿元;
中的回归方程,分析2003年至2012年我国产业差值的变化情况,并预测我国产业差值在哪一年约为34万亿元;
![]() 结合折线图,试求出除去2007年产业差值后剩余的9年产业差值的平均值及方差
结合折线图,试求出除去2007年产业差值后剩余的9年产业差值的平均值及方差![]() 结果精确到
结果精确到![]() .
.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: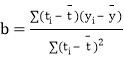 ,
,![]() .
.
样本方差公式:![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为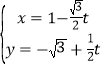 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校“凌云杯”篮球队的成员来自学校高一、高二共10个班的12位同学,其中高一(3)班、高二(3)各出2人,其余班级各出1人,这12人中要选6人为主力队员,则这6人来自不同的班级的概率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某老小区建成时间较早,没有集中供暖,随着人们生活水平的日益提高热力公司决定在此小区加装暖气该小区的物业公司统计了近五年(截止2018年年底)小区居民有意向加装暖气的户数,得到如下数据
年份编号x | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
加装户数y | 34 | 95 | 124 | 181 | 216 |
(Ⅰ)若有意向加装暖气的户数y与年份编号x满足线性相关关系求y与x的线性回归方程并预测截至2019年年底,该小区有多少户居民有意向加装暖气;
(Ⅱ)2018年年底郑州市民生工程决定对老旧小区加装暖气进行补贴,该小区分到120个名额物业公司决定在2019年度采用网络竞拍的方式分配名额,竞拍方案如下:①截至2018年年底已登记在册的居民拥有竞拍资格;②每户至多申请一个名额,由户主在竞拍网站上提出申请并给出每平方米的心理期望报价;③根据物价部门的规定,每平方米的初装价格不得超过300元;④申请阶段截止后,将所有申请居民的报价自高到低排列,排在前120位的业主以其报价成交;⑤若最后出现并列的报价,则认为申请时问在前的居民得到名额,为预测本次竞拍的成交最低价,物业公司随机抽取了有竞拍资格的50位居民进行调查统计了他们的拟报竞价,得到如图所示的频率分布直方图:

(1)求所抽取的居民中拟报竞价不低于成本价180元的人数;
(2)如果所有符合条件的居民均参与竞拍,请你利用样本估计总体的思想预测至少需要报价多少元才能获得名额(结果取整数)
参考公式对于一组数据(x1,y1),(x2,y2),(x3,y3),…(xn,yn),其回归直线![]() 的斜率和截距的最小二乘估计分别为,
的斜率和截距的最小二乘估计分别为,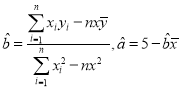
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究机构对某校学生往返校时间的统计资料表明:该校学生居住地到学校的距离![]() (单位:千米)和学生花费在上学路上的时间
(单位:千米)和学生花费在上学路上的时间![]() (单位:分钟)有如下的统计资料:
(单位:分钟)有如下的统计资料:
到学校的距离 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花费的时间 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明![]() 与
与![]() 有线性相关关系,试求:
有线性相关关系,试求:
(1)判断![]() 与
与![]() 是否有很强的线性相关性?
是否有很强的线性相关性?
(相关系数![]() 的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
(2)求线性回归方程![]() (精确到0.01);
(精确到0.01);
(3)将![]() 分钟的时间数据
分钟的时间数据![]() 称为美丽数据,现从这6个时间数据
称为美丽数据,现从这6个时间数据![]() 中任取2个,求抽取的2个数据全部为美丽数据的概率.
中任取2个,求抽取的2个数据全部为美丽数据的概率.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
参考公式: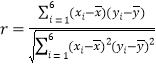 ,
,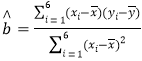
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人工景观湖外围有两条相互垂直的直线型公路ll,l2,且ll和l2交于点O.为了方便游客游览,计划修建一条连接公路与景观湖的直线型公路AB.景观湖的轮廓可以近似看成一个圆心为O,半径为2百米的圆,且公路AB与圆O相切,圆心O到ll,l2的距离均为5百米,设OAB=![]() ,AB长为L百米.
,AB长为L百米.
(1)求L关于![]() 的函数解析式;
的函数解析式;
(2)当![]() 为何值时,公路AB的长度最短?
为何值时,公路AB的长度最短?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com