
分析 (1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=$\sqrt{{a}^{2}+3}$sin(2ωx+φ),(其中,tanφ=$\frac{\sqrt{3}}{a}$),由f(x)的最大值为$\sqrt{{a}^{2}+3}$=2,解得a=1.又最小正周期为π.利用周期公式可得解得ω=1,即可得函数解析式,由2x+$\frac{π}{3}$=k$π+\frac{π}{2}$,k∈Z可解得对称轴方程.
(2)由$f({α-\frac{π}{6}})=\frac{4}{3}$,利用(1)结论可得sin2α=$\frac{2}{3}$,根据二倍角的余弦函数公式即可求值.
解答 解:(1)∵f(x)=2asinωxcosωx+2$\sqrt{3}{cos^2}ωx-\sqrt{3}({a>0,ω>0})$
=asin2ωx+$\sqrt{3}$cos2ωx
=$\sqrt{{a}^{2}+3}$sin(2ωx+φ),(其中,tanφ=$\frac{\sqrt{3}}{a}$),
∵f(x)的最大值为$\sqrt{{a}^{2}+3}$=2,解得:a=1.
又∵最小正周期为π.利用周期公式可得:$π=\frac{2π}{2ω}$,解得ω=1.
∴f(x)=2sin(2x+$\frac{π}{3}$),
∴由2x+$\frac{π}{3}$=k$π+\frac{π}{2}$,k∈Z可解得对称轴方程为:x=$\frac{kπ}{2}+\frac{π}{12}$,k∈Z.
(2)∵$f({α-\frac{π}{6}})=\frac{4}{3}$,
∴2sin[2($α-\frac{π}{6}$)+$\frac{π}{3}$]=2sin2α=$\frac{4}{3}$,解得:sin2α=$\frac{2}{3}$.
∴cos4α=1-2sin22α=1-2×$\frac{4}{9}$=$\frac{1}{9}$.
点评 本题主要考查了三角函数中的恒等变换应用,三角函数周期公式的应用,正弦函数的图象和性质,属于基本知识的考查.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
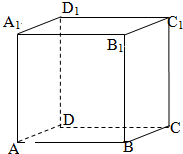 ABCD-A1B1C1D1是单位正方体,黑白两只蚂蚁从点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.白蚂蚁爬行的路线是AA1→A1D1,…,黑蚂蚁爬行的路线是AB→BB1,…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(i∈N*),设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处,则此时黑白蚂蚁的距离是( )
ABCD-A1B1C1D1是单位正方体,黑白两只蚂蚁从点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.白蚂蚁爬行的路线是AA1→A1D1,…,黑蚂蚁爬行的路线是AB→BB1,…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(i∈N*),设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处,则此时黑白蚂蚁的距离是( )| A. | $\sqrt{2}$ | B. | 1 | C. | 0 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 4 | C. | 10 | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱程度 | 非常喜欢 | 一般 | 不喜欢 |
| 人数 | 500 | 200 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com