
分析 (1)先令m=1,求得a3,n=m+2,求得a2,分类讨论n为奇数或偶数,分别求得通项公式,
(2)a2n-1+a2n+1与2a2n的通项公式,化简、比较大小,采用分析法,写出所以偶数项和奇数项整理即可.
解答 解:(1)令m=1,得$a_{n+1}^2a_{n-1}^2={n^2}-1$,从而$a_1^2a_3^2=3$,所以${a_3}=\sqrt{3}$,
令n=m+2,得$a_{2m+2}^2•a_2^2=4m+4$
从而${a_4}=\frac{{\sqrt{8}}}{a_2}$,${a}_{6}=\frac{\sqrt{12}}{{a}_{2}}$,又${a}_{4}{a}_{6}=\sqrt{{5}^{2}-1}$=$\sqrt{24}$,
∴${a}_{2}^{2}=2$,${a}_{2}=\sqrt{2}$,
从而${a}_{2m+1}=\sqrt{2m+1}$,
∴当n为偶数时,${a}_{n}=\sqrt{n}$;
令n=m+1,${a}_{2m+1}=\sqrt{2m+1}$,
可知当n为奇数时,${a_n}=\sqrt{n}$
综上可得${a_n}=\sqrt{n}$(n∈N+).
(2)(i)a2n-1+a2n+1-2a2n
=$(\sqrt{2n+1}-\sqrt{2n})+(\sqrt{2n-1}-\sqrt{2n})$
=$\frac{1}{\sqrt{2n+1}+\sqrt{2n}}-\frac{1}{\sqrt{2n-1}+\sqrt{2n}}$<0,
所以a2n-1+a2n+1<2a2n
(ii)即证明$\sqrt{2}+\sqrt{4}+…+\sqrt{2n}>\frac{n}{n+1}(\sqrt{1}+\sqrt{3}+\sqrt{5}+…+\sqrt{2n+1})$
由(i)得$\sqrt{1}+\sqrt{3}<2\sqrt{2}$,$\sqrt{3}+\sqrt{5}<2\sqrt{4}$,…,$\sqrt{2n-1}+\sqrt{2n+1}<2\sqrt{2n}$
将上述的n个式子相加,得$2(\sqrt{1}+\sqrt{3}+…+\sqrt{2n-1}+\sqrt{2n+1})-(1+\sqrt{2n+1})<2(\sqrt{2}+\sqrt{4}+…+\sqrt{2n})$
所以$\sqrt{2}+\sqrt{4}+…+\sqrt{2n}>(\sqrt{1}+\sqrt{3}+\sqrt{5}+…+\sqrt{2n+1})-\frac{{1+\sqrt{2n+1}}}{2}$,
所以,只需证$\sqrt{1}+\sqrt{3}+…+\sqrt{2n+1}≥\frac{{(n+1)(1+\sqrt{2n+1})}}{2}$,
事实上,当k=0,1,2,…,n时,
$\sqrt{1+2k}$+$\sqrt{2n+1-2k}$-1-$\sqrt{2n+1}$=$\frac{2k}{\sqrt{1+2k}+1}$-$\frac{2k}{\sqrt{2n+1-2k}+\sqrt{2n+1}}$≥0,
(∵$\sqrt{1+2k≤\sqrt{1+2n}}$,1$≤\sqrt{2n+1-2k}$),
∴$\sqrt{1+2k}+\sqrt{2n+1-2k}≥1+\sqrt{2n+1}$
从而$\sqrt{1}+\sqrt{3}+…+\sqrt{2n+1}=\frac{1}{2}[(1+\sqrt{2n+1})+(\sqrt{3}+\sqrt{2n-1})+…+(\sqrt{2n-1}+\sqrt{3})+(\sqrt{2n+1}+1)]$,
≥$\frac{1}{2}(n+1)(1+\sqrt{2n+1})$.
点评 本题考查求数列的通项公式及前n项和,采用分析法,进行不等式的证明,属于难题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
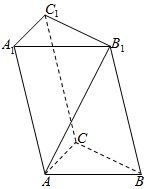 如图,在三棱柱ABC-A1B1C1中,AB=AC,且侧面BB1C1C是菱形,∠B1BC=60°.
如图,在三棱柱ABC-A1B1C1中,AB=AC,且侧面BB1C1C是菱形,∠B1BC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{\sqrt{11}}{2}$ | C. | 3 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{12}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com