
分析 (1)由题意可知an•bn=an-1•bn-1=…=a1•b1,故问题得以证明;
(2)根据{an}是递减数列,得到(a1-b1)2>0,an>bn,得到a1>b1恒成立,
(3)先判断an+1>2,再根据an+1-an=$\frac{4-{{a}_{n}}^{2}}{2{a}_{n}}$,得到an+1-an<0,{an}是递减数列,即可得到an-a2<0,求出an的取值范围.
解答 解:(1)∵$\left\{\begin{array}{l}{{a}_{n+1}=\frac{1}{2}{a}_{n}+\frac{1}{2}{b}_{n}}\\{\frac{1}{{b}_{n+1}}=\frac{1}{2}•\frac{1}{{a}_{n}}+\frac{1}{2}•\frac{1}{{b}_{n}}}\end{array}\right.$,
∴2an+1=an+bn,$\frac{1}{{b}_{n+1}}$=$\frac{{a}_{n}+{b}_{n}}{2{a}_{n}{b}_{{n}_{\;}}}$,
∴bn+1=$\frac{2{a}_{n}{b}_{n}}{{a}_{n}+{b}_{n}}$,
∴an+1bn+1=an•bn,
∴an•bn=an-1•bn-1=…=a1•b1,
∴{an•bn}是常数列;
(2){an}是递减数列,an+1-an<0,
∵a2-a1=$\frac{1}{2}$(a1+b1)-a1=$\frac{1}{2}$(b1-a1)<0
∴a1>b1,
∵a3-a2=$\frac{1}{2}$(b2-a2)<0,
∴a2>b2,
∵$\frac{1}{2}$(a1+b1)>$\frac{2{a}_{1}{b}_{1}}{{a}_{1}+{b}_{1}}$,
∴(a1-b1)2>0,
猜想an+1-an=$\frac{1}{2}$(bn-an)<0,
∴an>bn,
∴a1>b1恒成立,
∵ak+2-ak+1=$\frac{1}{2}$(bk+1-ak+1)=$\frac{\frac{2{a}_{k}{b}_{k}}{{a}_{k}+{b}_{k}}-\frac{{a}_{k}+{b}_{k}}{2}}{2}$=$\frac{-({a}_{k}-{b}_{k})^{2}}{4({a}_{k}+{b}_{k})}$<0,
∴a1>b1时,{an}是递减数列.
(3)整理得an+1=$\frac{1}{2}$(an+$\frac{4}{{a}_{n}}$),a1=4,
∴a2=$\frac{5}{2}$,
∴a1>0⇒a2>0⇒a3>0⇒…⇒an>0,
当n≥2时,an+1-2=$\frac{1}{2}$(an+$\frac{1}{{a}_{n}}$)-2=$\frac{({{a}_{n}}^{2}-2)^{2}}{2{a}_{n}}$>0,
∴an+1>2,
∴an+1-an=$\frac{1}{2}$(bn-an)=$\frac{\frac{4}{{a}_{n}}-{a}_{n}}{2}$=$\frac{4-{{a}_{n}}^{2}}{2{a}_{n}}$,
∵an>2,
∴an+1-an<0,
∴{an}是递减数列,
∴an-a2<0,
∴an∈(2,$\frac{5}{2}$]
点评 本题考查了递推数列的,常数列,数列的函数特征,以及an的取值范围,培养了学生的运算能力,转化能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
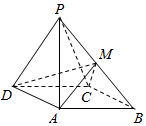 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | 2 | C. | 6 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.
如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份(x) | 2012 | 2013 | 2014 | 2015 | 2016 |
| 家庭数(y) | 6 | 10 | 16 | 22 | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com