
����С��13�֣�ij����������ҵΪ��ռ�и�����г��ݶ����2010��Ƚ���
һϵ�д�����������г�����Ͳ��㣬���ϵ���������x������������t��Ԫ������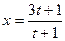 ����֪2010���������ϵ��豸�۾�
����֪2010���������ϵ��豸�۾� ��ά�ȹ̶�����Ϊ3 ��Ԫ��ÿ����1���
��ά�ȹ̶�����Ϊ3 ��Ԫ��ÿ����1���
��������Ͷ��32��Ԫ���������ã�����ÿ�����ϵ��ۼ۶�Ϊ���������ɱ���150%��ƽ��
ÿ�������ѵ�һ��֮�ͣ���������������������������ꡣ
��1����2010�������y����Ԫ����ʾΪ������t����Ԫ���ĺ�����
��2������ҵ2010��Ĵ�����Ͷ�������Ԫʱ����ҵ�����������
��ע������=�������롪���� �ɱ��������ѣ������ɱ�=�̶�����+�������ã�
�ɱ��������ѣ������ɱ�=�̶�����+�������ã�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪������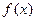 ��һ��ʵ��
��һ��ʵ��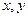 ����
����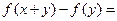
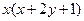 ��������
��������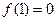 .
.
��1����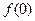 ��ֵ��
��ֵ��
��2����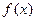 �Ľ���ʽ��
�Ľ���ʽ��
��3����֪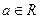 ����P����
����P����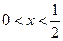 ʱ������ʽ
ʱ������ʽ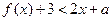 �������Q����
�������Q����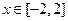 ʱ��
ʱ��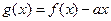 �ǵ����������������P������
�ǵ����������������P������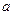 �ļ��ϼ�Ϊ
�ļ��ϼ�Ϊ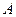 ������Q������
������Q������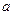 �ļ��ϼ�Ϊ
�ļ��ϼ�Ϊ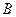 ����
����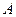 ��
��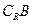 ��
��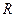 Ϊȫ������
Ϊȫ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
(��С������15��)��֪���κ��� ��
�� ������
������ ��
�� ���躯��
���躯��
�� ��
�� ����
����
��1���� �ı���ʽ��
�ı���ʽ��
��2���� ��ʹ
��ʹ
 ��������ʵ��
��������ʵ�� ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���� ��
�� ����֤������
����֤������ ������
������ .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���� �Ƕ�����
�Ƕ�����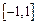 �ϵ��溯��,��
�ϵ��溯��,��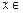
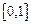 ʱ��
ʱ��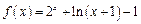 .
.
(1)���� �Ľ���ʽ�����ж�
�Ľ���ʽ�����ж� ��
��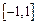 �ϵĵ�����(��Ҫ��֤��)��
�ϵĵ�����(��Ҫ��֤��)��
(2)�ⲻ��ʽ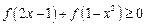 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��12�֣���֪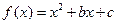 Ϊż����������
Ϊż����������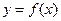 ����
����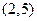 ��
��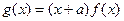 ��
��
��1��������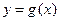 ����б��Ϊ0�����ߣ���ʵ��
����б��Ϊ0�����ߣ���ʵ�� ��ȡֵ��Χ��
��ȡֵ��Χ��
��2������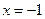 ʱ����
ʱ����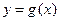 ȡ�ü�ֵ��ȷ��
ȡ�ü�ֵ��ȷ��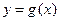 �ĵ������䣮
�ĵ������䣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com