
分析 要证明平行四边形的对角线互相平分,可以根据向量的模长相等进行证明;根据题意画出图形,结合平面向量的线性运算即可证明结论成立.
解答 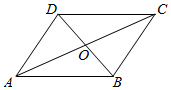 证明:设O为平行四边形ABCD对角线的交点,如图所示;
证明:设O为平行四边形ABCD对角线的交点,如图所示;
则$\overrightarrow{AB}$=$\overrightarrow{DC}$,$\overrightarrow{OB}$-$\overrightarrow{OA}$=$\overrightarrow{OC}$-$\overrightarrow{OD}$,
∴$\overrightarrow{OB}$+$\overrightarrow{OD}$=$\overrightarrow{OC}$+$\overrightarrow{OA}$=$\overrightarrow{0}$,
即$\overrightarrow{OB}$=-$\overrightarrow{OD}$,$\overrightarrow{OC}$=-$\overrightarrow{OA}$,
∴|$\overrightarrow{OB}$|=|$\overrightarrow{OD}$|,|$\overrightarrow{OC}$|=|$\overrightarrow{OA}$|,
即AC、BD互相平分;
故“平行四边形的对角线互相平分”.
点评 本题考查了利用向量法证明线段平行与相等的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:填空题
如图,在等边 中,
中, ,点
,点 是
是 边上的动点,点
边上的动点,点 关于直线
关于直线 ,
, 的对称点分别为
的对称点分别为 ,则线段
,则线段 长的取值范围是 .
长的取值范围是 .

查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:选择题
如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是( )
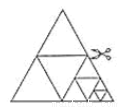
A.25 B.33 C.34 D.50
查看答案和解析>>
科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(理)试卷(解析版) 题型:解答题
已知向量 ,记
,记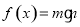 .
.
(1)若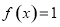 ,求
,求 的值;
的值;
(2)在锐角 中,角
中,角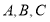 的对边分别是
的对边分别是 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com