
分析 由等差数列的性质和求和公式可得等差数列{an}的前7项为正数,从第8项开始为负数,可得结论.
解答 解:∵等差数列{an}的前n项和是Sn,且S14>0,S15<0,
∴S14=$\frac{14({a}_{1}+{a}_{14})}{2}$=7(a1+a14)=7(a7+a8)>0,即a7+a8>0,
S15=$\frac{15({a}_{1}+{a}_{15})}{2}$=$\frac{15×2{a}_{8}}{2}$=15a8<0,即a8<0,∴a7>0
∴等差数列{an}的前7项为正数,从第8项开始为负数,
∴在S1,S2,…中最大的是前7项的和
故答案为:7.
点评 本题考查等差数列的前n项和的最值,得出等差数列{an}的前7项为正数,从第8项开始为负数是解决问题的关键,属基础题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,过点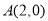 的直线
的直线 与
与 轴交于点
轴交于点 ,
,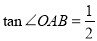 ,直线
,直线 上的点
上的点 位于
位于 轴左侧,且到
轴左侧,且到 轴的距离为1.
轴的距离为1.
(1)求直线 的表达式;
的表达式;
(2)若反比例函数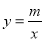 的图象经过点
的图象经过点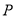 ,求
,求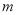 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
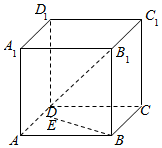 如图,已知正方体ABCD-A1B1C1D1中,E是平面ABCD上一动点,则直线BE与直线B1D所成角的余弦值的取值范围是[0,$\frac{\sqrt{6}}{3}$].
如图,已知正方体ABCD-A1B1C1D1中,E是平面ABCD上一动点,则直线BE与直线B1D所成角的余弦值的取值范围是[0,$\frac{\sqrt{6}}{3}$].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
已知直线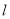 的参数方程为
的参数方程为 (
(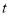 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,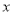 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线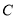 的极坐标方程为
的极坐标方程为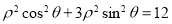 ,且曲线
,且曲线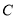 的左焦点
的左焦点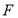 在直线
在直线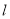 上.
上.
(1)若直线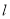 与曲线
与曲线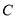 交于
交于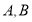 两点,求
两点,求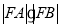 的值;
的值;
(2)求曲线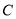 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com