
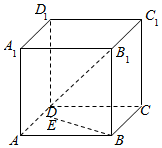
 如图,已知正方体ABCD-A1B1C1D1中,E是平面ABCD上一动点,则直线BE与直线B1D所成角的余弦值的取值范围是[0,$\frac{\sqrt{6}}{3}$].
如图,已知正方体ABCD-A1B1C1D1中,E是平面ABCD上一动点,则直线BE与直线B1D所成角的余弦值的取值范围是[0,$\frac{\sqrt{6}}{3}$]. 分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出直线BE与直线B1D所成角的余弦值的取值范围.
解答 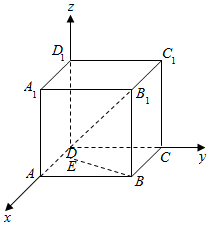 解以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为1,E(x,y,0),0≤x≤1,0≤y≤1,
则D(0,0,0),B(1,1,0),B1(1,1,1),
$\overrightarrow{BE}$=(x-1,y-1,0),$\overrightarrow{{B}_{1}D}$=(-1,-1,-1),
设直线BE与直线B1D所成角为θ,
cosθ=$\frac{|\overrightarrow{BE}•\overrightarrow{{B}_{1}D}|}{|\overrightarrow{BE}|•|\overrightarrow{{B}_{1}D}|}$=$\frac{(1-x)+(1-y)}{\sqrt{(x-1)^{2}+(y-1)^{2}}•\sqrt{3}}$,
∵0≤x≤1,0≤y≤1,
∴x=y=0时,(cosθ)max=$\frac{2}{\sqrt{2}•\sqrt{3}}$=$\frac{\sqrt{6}}{3}$.
当BE⊥BD时,(cosx)min=0.
∴直线BE与直线B1D所成角的余弦值的取值范围是[0,$\frac{\sqrt{6}}{3}$].
点评 本题考查异面直线所成角的取值范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:选择题
如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是( )
A.25 B.33 C.34 D.50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com