
分析 (1)如图所示,设抛物线C的方程为:y2=2px(p>0),直线AB的方程为ty+m=x,A(x1,y1),B(x2,y2).与抛物线方程可得根与系数的关系,即可得出.
(2)由(1)可得:直线AB的方程为ty+4=x,A(x1,y1),B(x2,y2).与抛物线方程联立可得根与系数的关系,只要证明$\overrightarrow{OA}•\overrightarrow{OB}$=0即可.
解答 (1)解:如图所示,
设抛物线C的方程为:y2=2px(p>0),直线AB的方程为ty+m=x,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{ty+m=x}\\{{y}^{2}=2px}\end{array}\right.$,化为y2-2pty-2pm=0,
∴y1y2=-2pm,
∴|-2pm|=4m,m>0,p>0,解得p=2.
∴抛物线C的方程为y2=4x;
(2)证明:由(1)可得:直线AB的方程为ty+4=x,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{ty+4=x}\\{{y}^{2}=4x}\end{array}\right.$,化为y2-4ty-16=0,
∴y1+y2=4t,y1y2=-16.
x1x2=(ty1+4)(ty2+4)=t2y1y2+4t(y1+y2)+16,
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=(t2+1)y1y2+4t(y1+y2)+16=-16(t2+1)+16t2+16=0,
∴OA⊥OB.
点评 本题考查了抛物线的标准及其性质、直线与抛物线相交问题转化为方程联立可得根与系数的关系、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源:2017届云南曲靖市高三上半月考一数学试卷(解析版) 题型:解答题
已知命题 :指数函数
:指数函数 在
在 上单调递减,命题
上单调递减,命题 :关于
:关于 的方程
的方程 的两个实根均大于
的两个实根均大于 .若
.若 或
或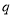 为真,
为真, 且
且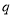 为假,求实数
为假,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-2x | B. | y=3x | C. | y=-3x | D. | y=4x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图:一个周长为1的圆沿着边长为2的正方形的边按逆时针方向滚动(无滑动),P是圆上的一定点,开始时PA⊥AB,当圆滚过正方形一周,回到起点时,点P所绘出的图形大致是( )
如图:一个周长为1的圆沿着边长为2的正方形的边按逆时针方向滚动(无滑动),P是圆上的一定点,开始时PA⊥AB,当圆滚过正方形一周,回到起点时,点P所绘出的图形大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分且不必要条件 | ||
| C. | 必要且不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com