
已知7件产品中有2件次品,现逐一不放回地进行检验,直到2件次品都能被确认为止.
(1)求检验次数为4的概率;
(2)设检验次数为ξ,求ξ的分布列和数学期望.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
如图所示,在A,B间有四个焊接点1,2,3,4,若焊接点脱落导致断路,则电路不通.今发现A,B之间线路不通,则焊接点脱落的不同情况有( )

A.9种 B.11种
C.13种 D.15种
查看答案和解析>>
科目:高中数学 来源: 题型:
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.
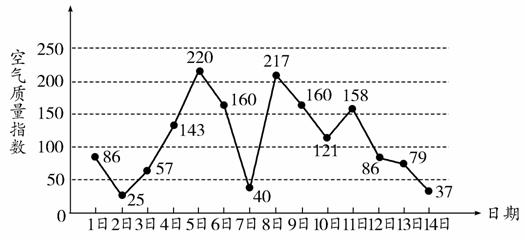
(1)求此人到达当日空气重度污染的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
| 降水量X | X<300 | 300≤X<700 | 700≤X<900 | X≥900 |
| 工期延误天数Y | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量X小于300、700、900的概率分别为0.3、0.7、0.9.求:
(1)工期延误天数Y的均值与方差;
(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
设z1、z2是复数,则下列命题中的假命题是( )
A.若|z1-z2|=0,则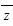 1=
1=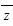 2
2
B.若z1=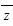 2,则
2,则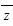 1=z2
1=z2
C.若|z1|=|z2|,则z1·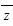 1=z2·
1=z2·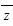 2
2
D.若|z1|=|z2|,则z =z
=z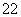
查看答案和解析>>
科目:高中数学 来源: 题型:
以下是对命题“若两个正实数a1,a2满足a +a
+a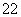 =1,则a1+a2≤
=1,则a1+a2≤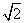 ”的证明过程:证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤
”的证明过程:证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤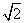 .
.
根据上述证明方法,若n个正实数a1、a2、…、an满足a +a
+a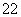 +…+a
+…+a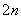 =1时,你能得到的结论为____________________(不必证明).
=1时,你能得到的结论为____________________(不必证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com