
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.
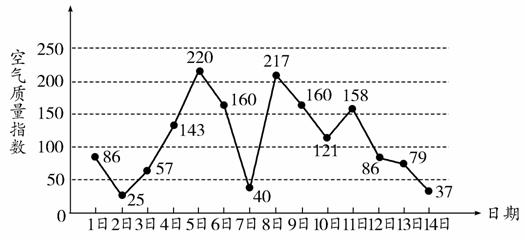
(1)求此人到达当日空气重度污染的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
设Ai表示事件“此人于3月i日到达该市”(i=1,2,…,13),
根据题意,P(Ai)=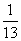 ,且Ai∩Aj=∅(i≠j).
,且Ai∩Aj=∅(i≠j).
(1)设B为事件“此人到达当日空气重度污染”,则B=A5∪A8,
所以P(B)=P(A5∪A8)=P(A5)+P(A8)=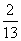 .
.
(2)由题意可知,X的所有可能取值为0,1,2,且
P(X=1)=P(A3∪A6∪A7∪A11)
=P(A3)+P(A6)+P(A7)+P(A11)= ,
,
P(X=2)=P(A1∪A2∪A12∪A13)
=P(A1)+P(A2)+P(A12)+P(A13)= ,
,
P(X=0)=1-P(X=1)-P(X=2)=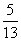 .
.
所以X的分布列为:
| X | 0 | 1 | 2 |
| P |
|
|
|


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
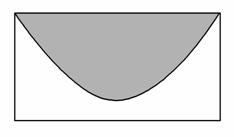
如图的矩形长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,由此我们可以估计出阴影部分的面积约为( )
A.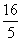 B.
B.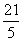
C.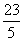 D.
D.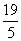
查看答案和解析>>
科目:高中数学 来源: 题型:
某机械零件加工由2道工序组成,第1道工序的废品率为a,第2道工序的废品率为b,假定这2道工序出废品的概率彼此无关,那么产品的合格率是( )
A.ab-a-b+1 B.1-a-b
C.1-ab D.1-2ab
查看答案和解析>>
科目:高中数学 来源: 题型:
已知7件产品中有2件次品,现逐一不放回地进行检验,直到2件次品都能被确认为止.
(1)求检验次数为4的概率;
(2)设检验次数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
抛掷一枚均匀的正方体骰子,观察出现的点数,如果出现了5点或6点,则称“抛掷高效”,若“抛掷高效”则得1分,否则得0分,则抛掷一次得分的期望为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com